题目内容
20.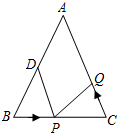 如图,已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
如图,已知△ABC中,AB=AC=10厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q以每秒$\frac{15}{4}$厘米的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
分析 (1)根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等;
(2)根据题意得出方程,求出t,根据路程求出即可.
解答 解:(1)全等,
理由是:∵t=1秒,
∴BP=CQ=3×1=3厘米,
∵AB=5厘米,点D为AB的中点,
∴BD=4厘米.
又∵PC=BC-BP,BC=8厘米,
∴PC=8-3=5厘米,
∴PC=BD.
又∵AB=AC,
∴∠B=∠C,
在△BPD和△CQP中,$\left\{\begin{array}{l}{BD=PC}\\{∠B=∠C}\\{BP=CQ}\end{array}\right.$
∴△BPD≌△CQP(SAS);
(2)设经过t秒P、Q相遇,
则3t+20=$\frac{15}{4}$t,
解得:t=$\frac{80}{3}$,
3×$\frac{80}{3}$=80,
∵AB=AC=10厘米,BC=8厘米,
∴P、Q在AB上相遇.
点评 本题考查了全等三角形的性质和判定,解一元一次方程的应用,能求出△BPD≌△CQP是解此题的关键,注意:全等三角形的对应边相等,对应角相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.下列说法不正确的是( )
| A. | 能够完全重合的两个图形是全等形 | |
| B. | 形状相同的两个图形是全等形 | |
| C. | 大小不同的两个图形不是全等形 | |
| D. | 形状、大小都相同的两个图形是全等形 |
11.某区中学生足球赛共赛8轮(即每队均参赛8 场),胜一场得3分,平一场得1分,输一场得0分,在这次足球联赛中,猛虎足球队踢平的场数是所负场数的2倍,共得17分,则该队胜了( )场.
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
15.若一个多边形的每一个外角都是60°,则这个多边形的内角和为( )
| A. | 1080° | B. | 180° | C. | 360° | D. | 720° |
9.在数轴上与表示-2的点距离等于3的点所表示的数是( )
| A. | 1 | B. | 5 | C. | 1或5 | D. | 1或-5 |
 如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′位置,AB′与CD交于点E,且AB=8,AD=4.
如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′位置,AB′与CD交于点E,且AB=8,AD=4.