题目内容
9.已知关于x的方程x2+2x+m=0.(1)当m=3时,方程的根的情况是没有实数根;
(2)当m=-3时,方程的根的情况是有两个不相等的实数根.
分析 (1)将m=3代入x2+2x+m=0,求出根的判别式△=b2-4ac的值,再根据判别式的意义即可求解;
(2)将m=-3代入x2+2x+m=0,求出根的判别式△=b2-4ac的值,再根据判别式的意义即可求解.
解答 解:(1)将m=3代入x2+2x+m=0,得x2+2x+3=0,
∵a=1,b=2,c=3,
∴△=b2-4ac=22-4×1×3=-8<0,
∴方程没有实数根;
(2)将m=-3代入x2+2x+m=0,得x2+2x-3=0,
∵a=1,b=2,c=-3,
∴△=b2-4ac=22-4×1×(-3)=16>0,
∴方程有两个不相等的实数根.
故答案为没有实数根;有两个不相等的实数根.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
1. 如图,下列语句正确的是( )
如图,下列语句正确的是( )
 如图,下列语句正确的是( )
如图,下列语句正确的是( )| A. | 线段AB与线段BC是同一条线段 | B. | 直线AB与直线是BC同一条直线 | ||
| C. | 点A在线段BC上 | D. | 点C在射线BA上 |
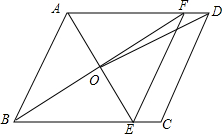 如图,在平行四边形ABCD中,AE平分∠BAD交BC于点E,BF平分∠ABC交AD于点F,AE、BF交于点O,连接EF、OD.
如图,在平行四边形ABCD中,AE平分∠BAD交BC于点E,BF平分∠ABC交AD于点F,AE、BF交于点O,连接EF、OD.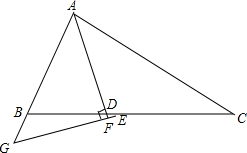 已知:△ABC中,∠ABC=2∠ACB,AD是∠BAC的角平分线,E是BC的中点,过E作EF⊥AD交AD的延长线于F,交AB的延长线于G,求证:BD=2BG.
已知:△ABC中,∠ABC=2∠ACB,AD是∠BAC的角平分线,E是BC的中点,过E作EF⊥AD交AD的延长线于F,交AB的延长线于G,求证:BD=2BG.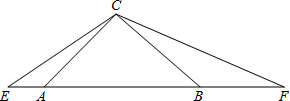 如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.
如图,在等腰三角形ABC中,∠ACB=90°,分别延长BA至点E,AB至点F,使得AE=2,且∠ECF=135°,若设AB=x,BF=y,试求出y与x之间的两数关系式.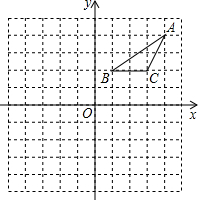 在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题:
在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题: