题目内容
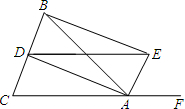 如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE.
如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE.考点:矩形的判定与性质
专题:证明题
分析:先由角平分线和等腰三角形的性质证明AE∥BD,再由AD、AE分别是∠BAC与∠BAC的外角的平分线可证得DA⊥AE,可得AD∥BE,可证得四边形ADBE为矩形,可得结论.
解答:证明:∵AD、AE分别是∠BAC与∠BAC的外角的平分线,
∴∠BAD+∠EAB=
(∠BAC+∠FAB)=90°,
∵BE⊥AE,
∴DA∥BE,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠FAB=∠ABC+∠ACB=2∠ABC,且∠FAB=2∠EAB,
∴∠ABC=∠EAB,
∴AE∥BD,
∴四边形AEBD为平行四边形,且∠BEA=90°,
∴四边形AEBD为矩形,
∴AB=DE.
∴∠BAD+∠EAB=
| 1 |
| 2 |
∵BE⊥AE,
∴DA∥BE,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠FAB=∠ABC+∠ACB=2∠ABC,且∠FAB=2∠EAB,
∴∠ABC=∠EAB,
∴AE∥BD,
∴四边形AEBD为平行四边形,且∠BEA=90°,
∴四边形AEBD为矩形,
∴AB=DE.
点评:本题主要考查矩形的判定和性质,由角平分线及等腰三角形的性质证明AE∥BD是解题的关键.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
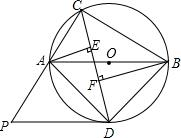 如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明.
如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明. 如图,CA、CD分别与⊙O相切于A、D,AB为⊙O的直径,CO的延长线交⊙O于E,求证:∠B=2∠BDE.
如图,CA、CD分别与⊙O相切于A、D,AB为⊙O的直径,CO的延长线交⊙O于E,求证:∠B=2∠BDE. 如图所示,在⊙O中,AB是直径,BD是弦,半径OC∥BD,求证:
如图所示,在⊙O中,AB是直径,BD是弦,半径OC∥BD,求证: