题目内容
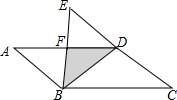 如图,已知四边形ABCD是一张平行四边形纸片,BD是一条对角线,且BD⊥DC,现沿BD将纸片翻折,使C点到达E点.
如图,已知四边形ABCD是一张平行四边形纸片,BD是一条对角线,且BD⊥DC,现沿BD将纸片翻折,使C点到达E点.(1)求证:以B,D,E,A为顶点的四边形是平行四边形.
(2)求证:FD
| ∥ |
. |
| 1 |
| 2 |
(3)若?ABCD的面积为20,求阴影部分的面积.
考点:平行四边形的判定与性质,三角形中位线定理,翻折变换(折叠问题)
专题:
分析:(1)根据折叠的性质证明E、D、C在同一直线上,根据对称的性质可以得到DC=DE,证明以B,D,E,A为顶点的四边形是平行四边形;
(2)根据平行四边形的对角线互相平分,以及平行四边形的对边相等即可证得;
(3)根据平行四边形的性质以及三角形的面积公式即可求解.
(2)根据平行四边形的对角线互相平分,以及平行四边形的对边相等即可证得;
(3)根据平行四边形的性质以及三角形的面积公式即可求解.
解答:(1)证明:∵BD⊥DC,即∠BDC=90°,
又∵△BCD和△BED关于BD对称,
∴∠BDE=∠BDC=90°,DE=DC,
∴E、D、C在同一直线上,
又∵平行四边形ABCD中,AB∥CD,
∴AB∥DE,且AB=DE,
∴以B,D,E,A为顶点的四边形是平行四边形;
(2)证明:∵四边形ABDE是平行四边形,
∴DF=AF,AD=BC,且AD∥BC,
∴FD
BC;
(3)解:S△ABD=
S平行四边形ABCD=
×20=10,
∵F是AD的中点,
∴S阴影=
S△ABD=
×10=5.
又∵△BCD和△BED关于BD对称,
∴∠BDE=∠BDC=90°,DE=DC,
∴E、D、C在同一直线上,
又∵平行四边形ABCD中,AB∥CD,
∴AB∥DE,且AB=DE,

∴以B,D,E,A为顶点的四边形是平行四边形;
(2)证明:∵四边形ABDE是平行四边形,
∴DF=AF,AD=BC,且AD∥BC,
∴FD
| ∥ |
. |
| 1 |
| 2 |
(3)解:S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
∵F是AD的中点,
∴S阴影=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了平行四边形的判定与性质,解决本题的关键是证明E、D、C在同一直线上.

练习册系列答案
相关题目
下面四个数中,最小的数是( )
| A、-2 | ||
| B、0 | ||
| C、0.2 | ||
D、-
|
 如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为( )
如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(-1,2),则点P的坐标为( )| A、(-4,0) |
| B、(-3,0) |
| C、(-2,0) |
| D、(-1.5,0) |
 如图,已知直线AB、DE相交于点O,∠AOC=160°,OC平分∠EOB,试求∠AOD的度数.
如图,已知直线AB、DE相交于点O,∠AOC=160°,OC平分∠EOB,试求∠AOD的度数.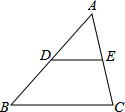 如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为
如图,在△ABC中,D、E分别是AB、AC的中点,若△ABC的面积为  如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,你知道BE与AC有什么位置关系吗,请说明理由.
如图,AD为△ABC的高,E为AC上一点,BE交AD于F,且有BF=AC,FD=CD,你知道BE与AC有什么位置关系吗,请说明理由. 如图,李老师在黑板上画了一个图形,请你在这个图形中分别找出角A的一个同位角、内错角和同旁内角,并指出是哪两条直线被哪条直线所截形成的.
如图,李老师在黑板上画了一个图形,请你在这个图形中分别找出角A的一个同位角、内错角和同旁内角,并指出是哪两条直线被哪条直线所截形成的.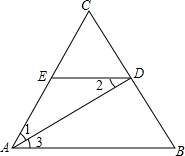 已知,如图,AD平分∠CAB,DE∥AB,求证:∠1=∠2.
已知,如图,AD平分∠CAB,DE∥AB,求证:∠1=∠2.