题目内容
13.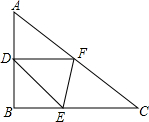 如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、F分别为AB、AC的中点,E是BC上动点,则△DEF周长的最小值为( )
如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、F分别为AB、AC的中点,E是BC上动点,则△DEF周长的最小值为( )| A. | 2+$\sqrt{10}$ | B. | 2+$\sqrt{13}$ | C. | $\sqrt{13}$ | D. | 6 |
分析 首先由三角形的中位线定理可求得DF的长为2,然后作出点F关于BC的对称点F′,连接DF′交BC于点E,由轴对称图形的性质可知EF=EF′,从而可得到ED+EF=DF′,然后在Rt△DFF′中,由勾股定理可求得DF′的长度,从而可求得三角形DEF的周长.
解答 解:如图,作点F关于BC的对称点F′,连接DF′交BC于点E.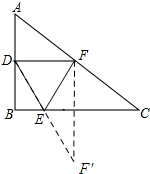
∵点D、F分别是AB和AC的中点,
∴DF=$\frac{1}{2}$BC=2.
∵点F与点F′关于BC对称,
∴EF=EF′
在Rt△DFF′中,DF′=$\sqrt{D{F}^{2}+FF{′}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$
△DEF的周长=DF+DE+EF=DF+DF′=2+$\sqrt{13}$.
故选:B.
点评 本题主要考查的是轴对称路径最短问题,作出点F关于BC的对称点,将DE+EF转化为DF′的长是解题的关键.

练习册系列答案
相关题目
5.对于非零的两个实数a、b,规定a⊕b=$\frac{1}{b}$-$\frac{1}{a}$.若1⊕(x+1)=1,则x的值为( )
| A. | $\frac{3}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |

 如图所示,在△ABC中,AB=AC,点D是底边BC上的一个动点,过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F.
如图所示,在△ABC中,AB=AC,点D是底边BC上的一个动点,过点D作BC的垂线分别交一腰和另一腰的延长线于点E、F.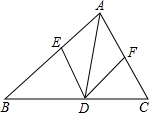 如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )