题目内容
1.请写出一个图象的对称轴是直线x=1,且经过(0,1)点的二次函数的表达式:y=x2-2x+1.分析 由对称轴确定顶点的横坐标为1,由经过(0,1)点确定x=0时,y=1,根据二次函数的顶点式写出解析式.本题答案不唯一.
解答 解:∵抛物线的对称轴是直线x=1,
∴设抛物线的解析式为y=a(x-1)2+k,
∵经过(0,1)点,
∴令a=1,
∴抛物线的解析式为y=x2-2x+1,
故答案为y=x2-2x+1(答案不唯一).
点评 本题考查了二次函数的性质与系数的联系,关键是把系数与性质对应,选择合适的二次函数解析式表达.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
12.满足下列条件的三角形中,不是直角三角形的是( )
| A. | 三个内角比为1:2:1 | B. | 三边之比为1:2:$\sqrt{5}$ | ||
| C. | 三边之比为$\sqrt{3}$:2:$\sqrt{5}$ | D. | 三个内角比为1:2:3 |
9.二元一次方程x+2y=5在实数范围内的解( )
| A. | 只有1个 | B. | 只有2个 | C. | 只有3个 | D. | 有无数个 |
13.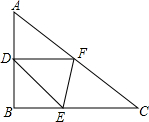 如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、F分别为AB、AC的中点,E是BC上动点,则△DEF周长的最小值为( )
如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、F分别为AB、AC的中点,E是BC上动点,则△DEF周长的最小值为( )
 如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、F分别为AB、AC的中点,E是BC上动点,则△DEF周长的最小值为( )
如图所示,已知Rt△ABC中,∠B=90°,AB=3,BC=4,D、F分别为AB、AC的中点,E是BC上动点,则△DEF周长的最小值为( )| A. | 2+$\sqrt{10}$ | B. | 2+$\sqrt{13}$ | C. | $\sqrt{13}$ | D. | 6 |
10. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,如果AC=12,BD=8,AB=x,那么x的取值范围是( )| A. | 2<x<10 | B. | 4<x<20 | C. | 8<x<12 | D. | 4<x<6 |
11.下面给出的是四边形ABCD中∠A、∠B、∠C、∠D的度数比,其中能判断出四边形是平行四边形的是( )
| A. | 4:3:2:1 | B. | 3:2:3:2 | C. | 3:3:2:2 | D. | 3:2:2:1 |