题目内容
4．已知$\left\{\begin{array}{l}{x+2y=4}\\{4x+3y=6}\end{array}\right.$，则x+y=2．分析 方程组中两方程相加即可求出x+y的值．
解答 解：$\left\{\begin{array}{l}{x+2y=4①}\\{4x+3y=6②}\end{array}\right.$，
①+②得：5（x+y）=10，
则x+y=2，
故答案为：2
点评 此题考查了解二元一次方程组，熟练掌握运算法则是解本题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
15．
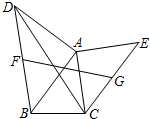如图，以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE，F、G分别是线段BD和CE的中点，则$\frac{CD}{FG}$的值等于（ ）
如图，以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE，F、G分别是线段BD和CE的中点，则$\frac{CD}{FG}$的值等于（ ）| A． | $\frac{{2\sqrt{3}}}{3}$ | B． | $\sqrt{2}$ | C． | $\frac{3}{2}$ | D． | $\sqrt{3}$ |
12．满足下列条件的三角形中，不是直角三角形的是（ ）
| A． | 三个内角比为1：2：1 | B． | 三边之比为1：2：$\sqrt{5}$ | ||
| C． | 三边之比为$\sqrt{3}$：2：$\sqrt{5}$ | D． | 三个内角比为1：2：3 |
19．在直角坐标系中，点P（-2，3）向右平移3个单位长度后的坐标为（ ）
| A． | （-2，6） | B． | （1，3） | C． | （1，6） | D． | （-5，3） |
9．二元一次方程x+2y=5在实数范围内的解（ ）
| A． | 只有1个 | B． | 只有2个 | C． | 只有3个 | D． | 有无数个 |
13．
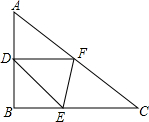如图所示，已知Rt△ABC中，∠B=90°，AB=3，BC=4，D、F分别为AB、AC的中点，E是BC上动点，则△DEF周长的最小值为（ ）
如图所示，已知Rt△ABC中，∠B=90°，AB=3，BC=4，D、F分别为AB、AC的中点，E是BC上动点，则△DEF周长的最小值为（ ）| A． | 2+$\sqrt{10}$ | B． | 2+$\sqrt{13}$ | C． | $\sqrt{13}$ | D． | 6 |
14．在函数y=$\sqrt{2-x}$中，自变量x的取值范围是（ ）
| A． | x≥2 | B． | x≤2 | C． | x＞2 | D． | x＜2 |