题目内容
14. (1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=$\sqrt{2}$.
(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=$\sqrt{2}$.(2)解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)根据整式乘法展开后合并同类项可得,将a、b的值代入计算可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)原式=a2-2ab+a2+2ab+b2
=2a2+b2,
将a=-1,b=$\sqrt{2}$代入上式,
得:原式=2×(-1)2+($\sqrt{2}$)2
=2+2
=4;
(2)解不等式4x>2x-6,得:x>-3,
解不等式$\frac{x-1}{3}≤\frac{x+1}{9}$,得:x≤2,
∴不等式组的解集为-3<x≤2,
在数轴上表示不等式组的解集为: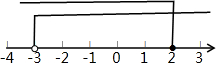
点评 本题主要考查整式的化简求值和解不等式组的基本能力,熟练进行整式的乘法运算和解不等式组的步骤是根本技能,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解不等式组的关键.

练习册系列答案
相关题目
4.已知矩形ABCD的边AB=a,AD=b(a>b>0),若点P为CD边上的一动点,且记DP=x,直线AP交BC的延长线于Q,使得DP+CQ为最小时,a,b、x应满足关系式为( )
| A. | x=$\frac{a+b}{2}$ | B. | x=$\sqrt{ab}$ | C. | a2-b2=x2 | D. | $\frac{1}{x}$=$\frac{1}{a}$+$\frac{1}{b}$ |
2.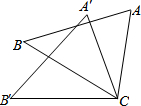 如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )
如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )
 如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )
如图,△ACB≌△A′C′B′,∠A=40°,则∠A′的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
9.下列运算错误的是( )
| A. | $\sqrt{18}$=3$\sqrt{2}$ | B. | 3$\sqrt{2}$×2$\sqrt{3}$=6$\sqrt{6}$ | C. | ($\sqrt{5}$+1)2=6 | D. | ($\sqrt{7}$+2)($\sqrt{7}$-2)=3 |
 如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点
如图,在直角坐标系中,经过点A(2,6)、点B(10,2)的直线与两条坐标轴分别相交于C、D两点,点P是x轴上的一点