题目内容
1.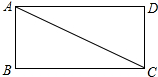 如图,在四边形ABCD中,AB=CD=6,BC=AD=8,AC=10.求证:四边形ABCD是矩形.
如图,在四边形ABCD中,AB=CD=6,BC=AD=8,AC=10.求证:四边形ABCD是矩形.
分析 根据AB=CD,BC=AD可得四边形ABCD是平行四边形,再利用勾股定理逆定理可得∠B=90°,根据有一个角是直角的平行四边形是矩形可得四边形ABCD是矩形.
解答 证明:∵AB=CD,BC=AD,
∴四边形ABCD是平行四边形,
∵62+82=102,
∴AB2+BC2=AC2,
∴∠B=90°,
∴四边形ABCD是矩形.
点评 此题主要考查了矩形的判定,关键是掌握矩形的判定定理:①矩形的定义:有一个角是直角的平行四边形是矩形;
②有三个角是直角的四边形是矩形;
③对角线相等的平行四边形是矩形(或“对角线互相平分且相等的四边形是矩形”).

练习册系列答案
相关题目
9.下列运算错误的是( )
| A. | $\sqrt{18}$=3$\sqrt{2}$ | B. | 3$\sqrt{2}$×2$\sqrt{3}$=6$\sqrt{6}$ | C. | ($\sqrt{5}$+1)2=6 | D. | ($\sqrt{7}$+2)($\sqrt{7}$-2)=3 |
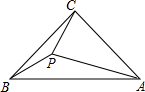 如图,等腰直角△ACB中,BC=AC=4,∠ACB=90°,点P为△ACB内一点,连BP,CP,若∠CBP=∠PCB=15°,则PA的长为4.
如图,等腰直角△ACB中,BC=AC=4,∠ACB=90°,点P为△ACB内一点,连BP,CP,若∠CBP=∠PCB=15°,则PA的长为4.
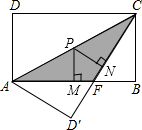 如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处.
如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处.