题目内容
3.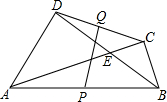 如图,四边形ABCD中,对角线AC与BD相交于点E,∠ADB=∠ACB=90°,P,Q分别是AB,CD的中点,给出下列结论:(1)PQ⊥CD;(2)AB=2PQ;(3)∠ADC与∠ABC互补.其中正确的是( )
如图,四边形ABCD中,对角线AC与BD相交于点E,∠ADB=∠ACB=90°,P,Q分别是AB,CD的中点,给出下列结论:(1)PQ⊥CD;(2)AB=2PQ;(3)∠ADC与∠ABC互补.其中正确的是( )| A. | (1)(2)(3) | B. | (1)(2) | C. | (1)(3) | D. | (2)(3) |
分析 连接PD、PC,根据直角三角形的性质、等腰三角形的性质解答即可.
解答 解: 连接PD、PC,
连接PD、PC,
∵∠ADB=∠ACB=90°,P是AB的中点,
∴PD=$\frac{1}{2}$AB,PC=$\frac{1}{2}$AB,
∴PD=PC,又Q是CD的中点,
∴PQ⊥CD,(1)符合题意;
∵AB=2PD,PD>PQ,
∴AB>2PQ,(2)不符合题意;
∵∠ADB=∠ACB=90°,
∴A、B、C、D四点共圆,
∴∠ADC与∠ABC互补,(3)符合题意,
故选:C.
点评 本题考查的是直角三角形的性质、等腰三角形的性质,掌握在直角三角形中,斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
4.某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?
(1)请你在下表的空格里填写一个适当的式子:
| 第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
| a | a+2 | a+4 | … |
(3)求当a=20时,第10排的座位数是多少?
5.把分式$\frac{100x}{x+y}$(x+y≠0)中的x,y同时扩大10倍,那么分式的值( )
| A. | 缩小10倍 | B. | 扩大10倍 | C. | 扩大100倍 | D. | 不改变 |
8.某学校七年级学生计划用义卖筹集的1160元钱购买古典名著《水浒传》和《西游记》共30套.小华查到网上图书商城的报价如图:

如果购买的《水浒传》尽可能的多,那么《水浒传》和《西游记》可以购买的套数分别是( )

如果购买的《水浒传》尽可能的多,那么《水浒传》和《西游记》可以购买的套数分别是( )
| A. | 20,10 | B. | 10,20 | C. | 21,9 | D. | 9,21 |
