如图.已知D.E分别是△ABC的边AB.AC的中点.则S△ADE:S四边形DECB=( )A．1:2B．1:3C．2:3D．1:4 题目和参考答案——青夏教育精英家教网—

题目内容

1．

如图，已知D、E分别是△ABC的边AB、AC的中点，则S_△ADE：S_{四边形DECB}=（　　）

A．

1：2

B．

1：3

C．

2：3

D．

1：4

分析由△ADE∽△ABC相似且相似比是1：2，相似三角形面积的比等于相似比的平方，即可解决问题．

解答解：∵D、E分别是△ABC的边AB、AC的中点，
∴DE∥BC，
∴△ADE∽△ABC，
∴AD：AB=1：2，
∴△ADE与△ABC的面积之比为1：4，
∴△ADE与四边形DBCE的面积之比是1：3．
故选B．

点评本题考查三角形的中位线定理、相似三角形的判定和性质等知识，解题关键是利用相似三角形面积的比等于相似比的平方解决问题，属于中考常考题型．

练习册系列答案

12．把数4、-3、-1.5、$2\frac{1}{2}$表示在数轴上，并将它们按从大到小的顺序排列．

9．如果汽车向东行驶30千米记作+30千米，那么-50千米表示向西行驶50千米．

16．

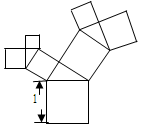有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了该图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2016次后形成的图形中所有的正方形的面积和是（　　）

	A．	明天是晴天		B．	打开电视，正在播放广告
	C．	三角形三个内角的和是180°		D．	两个负数的和是正数

13．在矩形ABCD中，AB=6cm，BC=8cm，点P从点A出发沿AB边以1cm/s的速度向点B移动，同时，点Q从点B出发沿BC以2cm、s的速度向点C移动，其中一点到达终点时，另一点随之停止运功．设运动时间为t秒：
（1）如图1，几秒后，△DPQ的面积等于21cm²？
（2）在运动过程中，若以P为圆心的⊙P同时与直线AD、BD相切（如图2），求t值；
（3）若以Q为圆心，PQ为半径作⊙Q．
①在运动过程中，是否存在t值，使得点D落在⊙Q上？若存在，求出t值；若不存在，请说明理由；
②若⊙Q与四边形CDPQ有三个公共点，则t的取值范围为0＜t＜4．（直接写出结果，不需说理）

10．【探究】中秋节前某商场计划购进一批进价为每盒40元的食品进行销售，根据销售经验，应季销售时，若每盒食品的售价为60元，则可售出400盒，当每盒食品的售价每提高1元，销售量就相应减少10盒．
（1）假设每盒食品的售价提高x元，那么销售每盒食品所获得的利润是20+x元，销售量是400-10x盒．（用含x为代数式表示）
（2）设应季销售利润为y元，求y与x的函数关系式，并求出应季销售利润为8000元时每盒食品的售价．
【拓展】根据销售经验，过季处理时，若每盒食品的售价定为30元亏本销售，可售出50盒，若每盒食品的售价每降低1元，销售量就相应增加5盒．当单价降低z元时，解答：
（1）现剩余100盒食品需要处理，经过降价处理后还是无法销售的只能积压在仓库，损失本金，若使亏损金额最小，此时每盒食品的售价应为20元；
（2）若过季需要处理的食品共m盒，过季处理时亏损金额为y₁元，求y₁与z的函数关系式；当100≤m≤300时，求过季销售亏损金额最小时多少元？

11．点P（-3，5）关于y轴的对称点P'的坐标是（　　）

试题分类