题目内容
8. 如图,已知△ABC∽△A′B′C′,且相似比为$\frac{AB}{A′B′}$=$\frac{3}{4}$,若AB=6,BC=5,AC=4,求△A′B′C′的周长.
如图,已知△ABC∽△A′B′C′,且相似比为$\frac{AB}{A′B′}$=$\frac{3}{4}$,若AB=6,BC=5,AC=4,求△A′B′C′的周长.
分析 设△A′B′C′的周长为x,根据相似三角形的周长比等于相似比得出方程,求出方程的解即可.
解答 解:设△A′B′C′的周长为x,
∵△ABC∽△A′B′C′,且相似比为$\frac{AB}{A′B′}$=$\frac{3}{4}$,AB=6,BC=5,AC=4,
∴$\frac{6+5+4}{x}$=$\frac{3}{4}$,
解得:x=20,
即△A′B′C′的周长为20.
点评 本题考查了相似三角形的性质的应用,能根据相似三角形的性质得出方程是解此题的关键,注意:相似三角形的周长比等于相似比.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
16.王慧同学不但会学习,而且也很会安排时间干好家务活,煲饭、炒菜、擦窗等样样都行,是爸爸妈妈的好帮手,某一天放学回家后,她完成各项家务活及所需时间如表:王慧同学完成以上各项家务活,至少需要33分钟.(注:各项工作转接时间忽略不计)
| 家务项目 | 擦窗 | 洗菜 | 洗饭煲、洗米 | 炒菜(用煤气炉) | 煲饭(用电饭煲) |
| 完成各项家务所需时间 | 5分钟 | 4分钟 | 3分钟 | 20分钟 | 30分钟 |
13.若△ABC和△DEF满足下列条件,其中使△ABC与△DEF相似的是( )
| A. | AB=6,BC=6,AC=9,DE=4,EF=4,DF=6 | |
| B. | AB=4,BC=6,AC=8,DE=5,EF=10,DF=15 | |
| C. | AB=1,BC=$\sqrt{2}$,AC=2,DE=$\sqrt{6}$,EF=$\sqrt{3}$,DF=$\sqrt{5}$ | |
| D. | AB=1,BC=$\sqrt{5}$,AC=3,DE=$\sqrt{15}$,EF=2$\sqrt{3}$,DF=$\sqrt{6}$ |
20.若方程(m-1)x2+x=1是关于x的一元二次方程,则m的取值范围是( )
| A. | m≠1 | B. | m≥0 | C. | m≥0且m≠1 | D. | m为任意正实数 |
17.下列判断中,正确的是( )
| A. | 0的绝对值是0 | B. | $\frac{22}{7}$是无理数 | C. | 4的平方根是2 | D. | 1的倒数是-1 |
18.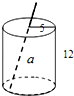 如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
 如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )
如图,是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,则一条到达底部的直吸管在罐内部分a的长度(罐壁的厚度和小圆孔的大小忽略不计)范围是( )| A. | 5≤a≤12 | B. | 5≤a≤13 | C. | 12≤a≤13 | D. | 12≤a≤15 |
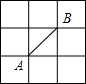 如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果点C也是图中的格点,且使得△ABC为等腰直角三角形,则点C的个数是( )
如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果点C也是图中的格点,且使得△ABC为等腰直角三角形,则点C的个数是( )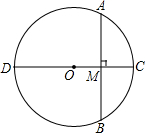 如图,圆O的直径CD=6cm,AB是圆O的弦AB⊥CD,垂足为M,OM:OD=3:5,求AB的长.
如图,圆O的直径CD=6cm,AB是圆O的弦AB⊥CD,垂足为M,OM:OD=3:5,求AB的长.