题目内容
6．
如图，已知A，B，C，D是⊙O上四点，若AC=BD，求证：AB=CD．
分析 根据在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等由AB=CD得到$\widehat{AB}$=$\widehat{CD}$，再利用等量加等量和相等得到$\widehat{AC}$=$\widehat{DB}$，于是有AC=BD．
解答 证明：∵AB=CD，
∴$\widehat{AB}$=$\widehat{CD}$，
∴$\widehat{AB}$+$\widehat{BC}$=$\widehat{CD}$+$\widehat{BC}$，即$\widehat{AC}$=$\widehat{BD}$，
∴AC=BD．
点评 本题考查了圆心角、弧、弦的关系：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等；在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．
练习册系列答案
相关题目
16．王慧同学不但会学习，而且也很会安排时间干好家务活，煲饭、炒菜、擦窗等样样都行，是爸爸妈妈的好帮手，某一天放学回家后，她完成各项家务活及所需时间如表：王慧同学完成以上各项家务活，至少需要33分钟．（注：各项工作转接时间忽略不计）
| 家务项目 | 擦窗 | 洗菜 | 洗饭煲、洗米 | 炒菜（用煤气炉） | 煲饭（用电饭煲） |
| 完成各项家务所需时间 | 5分钟 | 4分钟 | 3分钟 | 20分钟 | 30分钟 |
17．下列判断中，正确的是（ ）
| A． | 0的绝对值是0 | B． | $\frac{22}{7}$是无理数 | C． | 4的平方根是2 | D． | 1的倒数是-1 |
14．电影院的第3排第6座表示为（3，6）．若某同学的座位号为（4，2），那么该同学的位置是（ ）
| A． | 第2排第4座 | B． | 第4排第2座 | C． | 第4座第4排 | D． | 无法确定 |
1．
如图，一个机器人从O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2点，再向正西方向走9米到达A3点，再向正南方向走12米到达A4点，再向正东方向走15米到达A5点，按如此规律走下去，当机器人走到A6点时，则A6的坐标为（ ）
如图，一个机器人从O点出发，向正东方向走3米到达A1点，再向正北方向走6米到达A2点，再向正西方向走9米到达A3点，再向正南方向走12米到达A4点，再向正东方向走15米到达A5点，按如此规律走下去，当机器人走到A6点时，则A6的坐标为（ ）| A． | （9，15） | B． | （6，15） | C． | （9，9） | D． | （9，12） |
11．
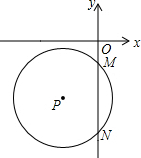如图，半径为5的⊙P与y轴交于点M（0，-4），N（0，-10），函数y=kx的图象经过点P，则k的值为（ ）
如图，半径为5的⊙P与y轴交于点M（0，-4），N（0，-10），函数y=kx的图象经过点P，则k的值为（ ）| A． | -$\frac{4}{7}$ | B． | -$\frac{7}{4}$ | C． | $\frac{4}{7}$ | D． | $\frac{7}{4}$ |
18．
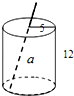如图，是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）
如图，是一个圆柱形饮料罐，底面半径是5，高是12，上底面中心有一个小圆孔，则一条到达底部的直吸管在罐内部分a的长度（罐壁的厚度和小圆孔的大小忽略不计）范围是（ ）| A． | 5≤a≤12 | B． | 5≤a≤13 | C． | 12≤a≤13 | D． | 12≤a≤15 |
16．在Rt△ABC中，如果各边的长度都扩大2倍，那么锐角A的正弦值与余弦值（ ）
| A． | 都不变 | B． | 都扩大2倍 | C． | 都缩小$\frac{1}{2}$ | D． | 以上都不对 |