题目内容
10．抛物线y=-x2+bx+c经过（-1，0）和（3，0）点，它的解析式为y=-x2+2x+3．分析 由抛物线y=-x2+bx+c经过（-1，0）和（3，0）点，利用待定系数法即可求得答案．
解答 解：∵抛物线y=-x2+bx+c经过（-1，0）和（3，0）点，
∴$\left\{\begin{array}{l}{-1-b+c=0}\\{-9+3b+c=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$，
∴它的解析式为：y=-x2+2x+3．
故答案为：y=-x2+2x+3．
点评 此题考查了待定系数法求二次函数的解析式．注意掌握待定系数法的应用．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
1．
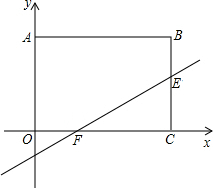如图所示，在平面直角坐标系中，长方形ABCO的边OA、OC分别在y轴、x轴上，OA=3，OC=4，直线y=$\frac{2}{3}$x-$\frac{2}{3}$与长方形ABCO的边OC、BC分别交于F、E，则△CEF的面积是（ ）
如图所示，在平面直角坐标系中，长方形ABCO的边OA、OC分别在y轴、x轴上，OA=3，OC=4，直线y=$\frac{2}{3}$x-$\frac{2}{3}$与长方形ABCO的边OC、BC分别交于F、E，则△CEF的面积是（ ）| A． | 6 | B． | 3 | C． | 12 | D． | $\frac{4}{3}$ |
2．下列各式与$\sqrt{3}$是同类二次根式的是（ ）
| A． | $\sqrt{9}$ | B． | $\sqrt{18}$ | C． | $\sqrt{12}$ | D． | $\sqrt{6}$ |
抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-1，其部分图象如图所示．已知ax2+bx+c=0的两个根分别为x1、x2，且x1＜x2，则x2的取值范围是0＜x2＜1．