题目内容
12.一个正比例函数的图象与反比例函数y=-$\frac{6\sqrt{3}}{x}$的图象交于A(x1,y1)B(x2,y2)两点,则(x2-x1)(y2-y1)的值为-24$\sqrt{3}$.分析 先根据解析式及图象上的点,则坐标满足解析式,得:x1y1=-6$\sqrt{3}$,x2y2=-6$\sqrt{3}$,由正比例函数的图象与反比例函数y=-$\frac{6\sqrt{3}}{x}$的图象的交点关于原点对称,得:x1=-x2,y1=-y2,将所求的式子化简后代入可得结论.
解答 解:∵A(x1,y1)B(x2,y2)两点在反比例函数y=-$\frac{6\sqrt{3}}{x}$的图象上,
∴x1y1=-6$\sqrt{3}$,x2y2=-6$\sqrt{3}$,且x1=-x2,y1=-y2,
∴(x2-x1)(y2-y1),
=x2y2-x2y1-x1y2+x1y1,
=-6$\sqrt{3}$+x1y1+x2y2-6$\sqrt{3}$,
=-24$\sqrt{3}$,
故答案为:-24$\sqrt{3}$.
点评 本题考查了反比例函数和正比例函数的交点问题,求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,明确正比例函数的图象与反比例函数y=-$\frac{6\sqrt{3}}{x}$的图象的交点关于原点对称.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.A,B是数轴上两点,点A,B表示的数可能互为相反数的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.
如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm. 如图,O为数轴原点,点A、B分别表示-2、2,以AB为底边向数轴上方作等腰三角形△ABC,连接OC,以O为圆心,OC长为半径画圆弧交数轴正半轴于点D,若AC=3,则点D表示的实数为$\sqrt{5}$.
如图,O为数轴原点,点A、B分别表示-2、2,以AB为底边向数轴上方作等腰三角形△ABC,连接OC,以O为圆心,OC长为半径画圆弧交数轴正半轴于点D,若AC=3,则点D表示的实数为$\sqrt{5}$. 如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).
如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).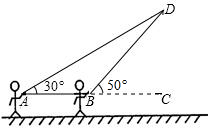 放风筝是大家喜爱的一种运动星期天的上午小明在金明广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为50°,已知点A,B,C在同一条水平直线上,小明搬了一把梯子来取风筝,梯子能达到的最大高度为20米,请问小明能把风筝捡回来吗?(最后结果精确到1米)(风筝线AD,BD均为线段,$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)
放风筝是大家喜爱的一种运动星期天的上午小明在金明广场上放风筝,如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为50°,已知点A,B,C在同一条水平直线上,小明搬了一把梯子来取风筝,梯子能达到的最大高度为20米,请问小明能把风筝捡回来吗?(最后结果精确到1米)(风筝线AD,BD均为线段,$\sqrt{3}$≈1.732,sin50°≈0.766,cos50°≈0.643,tan50°≈1.192)


