题目内容
7.随着“一带一路”的进一步推进,我国瓷器(“china”)更为“一带一路”沿线人民所推崇,一外国商户看准这一商机,向我国一瓷器经销商咨询工艺品茶具,得到如下信息:(1)每个茶壶的批发价比茶杯多110元;
(2)一套茶具包括一个茶壶与四个茶杯;
(3)600元批发茶壶的数量与160元批发茶杯的数量相同.
根据以上信息:
(1)求茶壶与茶杯的批发价;
(2)若该商户购进茶杯的数量是茶壶数量的5倍还多20个,并且总数不超过200个,该商户打算将一半的茶具按每套500元成套销售,其余按每个茶壶270元,每个茶杯70元零售,请帮助他设计一种获取利润最大的方案,并求出最大利润.
分析 (1)设茶杯的批发价为x元/个,则茶壶的批发价为(x+110)元/个,根据数量=总价÷单价结合600元批发茶壶的数量与160元批发茶杯的数量相同,即可得出关于x的分式方程,解之并检验后即可得出结论;
(2)设商户购进茶壶m个,则购进茶杯(5m+20)个,根据总数不超过200个,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,设利润为w,根据总利润=单件利润×销售数量结合销售方式,即可得出w关于m的函数关系式,利用一次函数的性质即可解决最值问题.
解答 解:(1)设茶杯的批发价为x元/个,则茶壶的批发价为(x+110)元/个,
根据题意得:$\frac{600}{x+110}$=$\frac{160}{x}$,
解得:x=40,
经检验,x=40是原分式方程的解,
∴x+110=150.
答:茶杯的批发价为40元/个,则茶壶的批发价为150元/个.
(2)设商户购进茶壶m个,则购进茶杯(5m+20)个,
根据题意得:m+5m+20≤200,
解得:m≤30.
若利润为w元,则w=$\frac{1}{2}$m(500-150-4×40)+$\frac{1}{2}$m×(270-150)+(5m+20-$\frac{1}{2}$×4m)×(70-40)=245m+600,
∵w随着m的增大而增大,
∴当m取最大值时,利润w最大,
当m=30时,w=7950.
∴当购进30个茶壶、170个茶杯时,有最大利润,最大利润为7950元.
点评 本题考查了一次函数的应用、分式方程的应用、一元一次不等式的应用以及一次函数的性质,解题的关键是:(1)根据数量=总价÷单价,列出关于x的分式方程;(2)根据数量关系,找出w关于m的函数关系式.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
12.下列运算正确的是( )
| A. | 2a3÷a=6 | B. | (a+b)(a-b)=a2-b2 | C. | (ab3)2=a2b5 | D. | (a+b)2=a2+b2 |
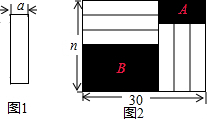 把六张形状大小完全相同的小长方形卡片(其中较短的一边长为a厘米,如图1)不重叠地放在一个底面为长方形(长为30cm,宽为ncm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分分别用A,B表示,请观察图形,回答问题:
把六张形状大小完全相同的小长方形卡片(其中较短的一边长为a厘米,如图1)不重叠地放在一个底面为长方形(长为30cm,宽为ncm)的盒子底部(如图2),盒子底面未被卡片覆盖的部分分别用A,B表示,请观察图形,回答问题:
 如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.
如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm. 图示为一个长方体盒子的表面展开图,CD=80cm,EF=70cm,设AB=x cm,这个长方体的表面积为y cm2
图示为一个长方体盒子的表面展开图,CD=80cm,EF=70cm,设AB=x cm,这个长方体的表面积为y cm2