题目内容
13.先化简,再求值:($\frac{1}{x-1}$-$\frac{1}{x+1}$)•(x-1),其中x=$\sqrt{2}$-1.分析 根据分式的减法和乘法可以化简题目中的式子,然后将x的值代入即可解答本题.
解答 解::($\frac{1}{x-1}$-$\frac{1}{x+1}$)•(x-1)
=$\frac{x+1-(x-1)}{(x-1)(x+1)}•(x-1)$
=$\frac{x+1-x+1}{x+1}$
=$\frac{2}{x+1}$,
当x=$\sqrt{2}-1$时,原式=$\frac{2}{\sqrt{2}-1+1}=\frac{2}{\sqrt{2}}=\sqrt{2}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式的化简求值的方法.

练习册系列答案
相关题目
5.下列事件是随机事件的是( )
| A. | 从装有22个红球、2个黄球的袋中摸出3个球,它们的颜色全不相同 | |
| B. | 通常温度降到0℃以下,纯净的水结冰 | |
| C. | 任意画一个三角形,其内角和是360° | |
| D. | 随意翻到一本书的某页,这页的页码是奇数 |
1.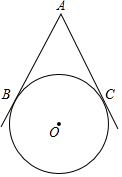 如图,AB、AC是◎o的两条切线,切点为B、C且∠BAC=50°,D是圆上一动点(不与B、C重合),则∠BDC的度数为( )
如图,AB、AC是◎o的两条切线,切点为B、C且∠BAC=50°,D是圆上一动点(不与B、C重合),则∠BDC的度数为( )
 如图,AB、AC是◎o的两条切线,切点为B、C且∠BAC=50°,D是圆上一动点(不与B、C重合),则∠BDC的度数为( )
如图,AB、AC是◎o的两条切线,切点为B、C且∠BAC=50°,D是圆上一动点(不与B、C重合),则∠BDC的度数为( )| A. | 130° | B. | 65° | C. | 50°或130° | D. | 65°或115° |
3.A,B是数轴上两点,点A,B表示的数可能互为相反数的是( )
| A. |  | B. |  | C. |  | D. |  |

 如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.
如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.