题目内容
 如图所示,AE⊥BE,AD⊥DC,CD=BE,∠DAB=∠EAC,求证:AB=AC.
如图所示,AE⊥BE,AD⊥DC,CD=BE,∠DAB=∠EAC,求证:AB=AC.考点:全等三角形的判定与性质
专题:证明题
分析:由AE⊥BE,AD⊥DC得到一对直角相等,再由已知角相等,利用等式的性质得到∠DAC=∠EAB,以及CD=BE,利用AAS得到三角形ACD与三角形ABE全等,利用全等三角形对应边相等即可得证.
解答:证明:∵AE⊥BE,AD⊥DC,
∴∠D=∠E=90°,
∵∠DAB=∠EAC,
∴∠DAB+∠ABC=∠EAC+∠ABC,即∠DAC=∠EAB,
在△ACD和△ABE中,
,
∴△ACD≌△EAB(AAS),
∴AB=AC.
∴∠D=∠E=90°,
∵∠DAB=∠EAC,
∴∠DAB+∠ABC=∠EAC+∠ABC,即∠DAC=∠EAB,
在△ACD和△ABE中,
|
∴△ACD≌△EAB(AAS),
∴AB=AC.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列四条直线是数轴的是( )
A、 |
B、 |
C、 |
D、 |
点A,B,P在同一直线上,下列说法正确的是( )
| A、若AB=2PA,则P是AB的中点 |
| B、若AB=PB,则P是AB的中点 |
| C、若AB=2PB,则P是AB的中点 |
| D、若AB=2PA=2PB,则P是AB的中点 |
已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=60°,∠BOC=20°,∠AOC的度数为( )
| A、40° | B、80° |
| C、20° | D、40°或80° |
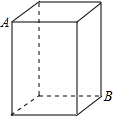 如图所示,有一个长、宽各2米,高为4米且封闭的长方体纸盒,一只昆虫从顶点A要爬到顶点B,那么这只昆虫爬行的最短路程为( )
如图所示,有一个长、宽各2米,高为4米且封闭的长方体纸盒,一只昆虫从顶点A要爬到顶点B,那么这只昆虫爬行的最短路程为( )| A、3米 | ||
| B、5米 | ||
C、4
| ||
D、2
|
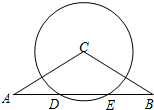 如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.
如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE. 如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长.
如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长. 作图:作图题
作图:作图题