题目内容
 如图,∠AOB=40°,OB⊥OC,OD、OE分别平分∠AOB和∠BOC,求∠EOD的度数.
如图,∠AOB=40°,OB⊥OC,OD、OE分别平分∠AOB和∠BOC,求∠EOD的度数.考点:垂线,角平分线的定义
专题:
分析:直接利用垂直的定义以及角平分线的定义得出∠DOB=20°,∠BOE=45°,进而得出答案.
解答:解:∵∠AOB=40°,OB⊥OC,OD、OE分别平分∠AOB和∠BOC,
∴∠DOB=20°,∠BOE=45°,
∴∠EOD=20°+45°=65°.
∴∠DOB=20°,∠BOE=45°,
∴∠EOD=20°+45°=65°.
点评:此题主要考查了角平分线的定义,得出∠DOB、∠BOE的度数是解题关键.

练习册系列答案
相关题目
已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=60°,∠BOC=20°,∠AOC的度数为( )
| A、40° | B、80° |
| C、20° | D、40°或80° |
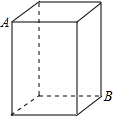 如图所示,有一个长、宽各2米,高为4米且封闭的长方体纸盒,一只昆虫从顶点A要爬到顶点B,那么这只昆虫爬行的最短路程为( )
如图所示,有一个长、宽各2米,高为4米且封闭的长方体纸盒,一只昆虫从顶点A要爬到顶点B,那么这只昆虫爬行的最短路程为( )| A、3米 | ||
| B、5米 | ||
C、4
| ||
D、2
|
比-3.1大的非正整数的个数是( )
| A、2 | B、3 | C、4 | D、5 |
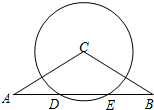 如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.
如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE. 在△ABC中,∠A=50°,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,求∠D的度数.
在△ABC中,∠A=50°,∠BEC=150°,∠ABE的平分线与∠ACE的平分线相交于点D,求∠D的度数.