题目内容
 如图,点M(2,2),将一个90°的角尺的直角顶点放在点M处,角尺的两边分别交x轴、y轴正半轴于A、B,AP平分∠OAB,交OM于点P,PN⊥x轴于N,把角尺绕点M旋转时:
如图,点M(2,2),将一个90°的角尺的直角顶点放在点M处,角尺的两边分别交x轴、y轴正半轴于A、B,AP平分∠OAB,交OM于点P,PN⊥x轴于N,把角尺绕点M旋转时:(1)求证:OM平分∠AOB;
(2)求OA+OB的值;
(3)ON+
| 1 |
| 2 |
考点:全等三角形的判定与性质,坐标与图形性质,角平分线的性质
专题:
分析:(1)做ME⊥x轴于E,MF⊥y轴于F,根据M的坐标得出MF=ME,根据角平分线性质得出即可;
(2)求出OA+OB=OF+OE,即可得出答案;
(3)过P作PQ⊥ME于Q,延长PQ到R,使QR=PQ,连接MR,求出AB=PR,求出ON+
AB=OE,即可得出答案.
(2)求出OA+OB=OF+OE,即可得出答案;
(3)过P作PQ⊥ME于Q,延长PQ到R,使QR=PQ,连接MR,求出AB=PR,求出ON+
| 1 |
| 2 |
解答:证明:(1)做ME⊥x轴于E,MF⊥y轴于F,
∵M(2,2),∠FOE=∠MEO=∠MFO=90°,
∴OEMF是正方形,OE=2,OF=2,
∴MF=ME,
∵ME⊥x轴于E,MF⊥y轴于F,
∴OM平分∠EOF,即OM平分∠AOB;
(2)∵∠AMF+∠AME=∠AME+∠BME=90°,
∴∠AMF=∠BME,
在△AME和△BMF中,
,
∴△AME≌△BMF(ASA),
∴AE=BF,
∴OA+OB=OA+OF+BF=OA+OF+AE=OE+OF=4;
(3)解:ON+
AB的值不会发生变化,
理由是:
过P作PQ⊥ME于Q,延长PQ到R,使QR=PQ,连接MR,
∵△AEM≌△BFM,
∴MB=MA,
∵∠AMB=90°,
∴∠MBA=∠MAB=45°,
∵OM平分∠AOB,AP平分∠BAO,∠BOA=90°,
∴∠∠MOA=45°,∠BAP=∠PAO,
∴∠∠MOA+∠PAO=∠MAB+∠BAP,
即∠MAP=∠MPA,
∴MP=MA,
∵∠MOE=45°,ME=OE=2,
∴∠OME=45°,
∵PR⊥ME,PQ=QR,
∴MP=MR,
∴MB=MP=MA=MR,
∴∠RMQ=∠PMQ=45°,
∴∠PMR=90°=∠BMA,
在△BMA和△PMR中,
,
∴△BMA≌△PMR(SAS),
∴AB=PR,
∴ON+
AB=ON+
PR=ON+PQ=OE=2,
即ON+
AB的值不会发生变化.

∵M(2,2),∠FOE=∠MEO=∠MFO=90°,
∴OEMF是正方形,OE=2,OF=2,
∴MF=ME,
∵ME⊥x轴于E,MF⊥y轴于F,
∴OM平分∠EOF,即OM平分∠AOB;
(2)∵∠AMF+∠AME=∠AME+∠BME=90°,
∴∠AMF=∠BME,
在△AME和△BMF中,
|
∴△AME≌△BMF(ASA),
∴AE=BF,
∴OA+OB=OA+OF+BF=OA+OF+AE=OE+OF=4;
(3)解:ON+
| 1 |
| 2 |
理由是:

过P作PQ⊥ME于Q,延长PQ到R,使QR=PQ,连接MR,
∵△AEM≌△BFM,
∴MB=MA,
∵∠AMB=90°,
∴∠MBA=∠MAB=45°,
∵OM平分∠AOB,AP平分∠BAO,∠BOA=90°,
∴∠∠MOA=45°,∠BAP=∠PAO,
∴∠∠MOA+∠PAO=∠MAB+∠BAP,
即∠MAP=∠MPA,
∴MP=MA,
∵∠MOE=45°,ME=OE=2,
∴∠OME=45°,
∵PR⊥ME,PQ=QR,
∴MP=MR,
∴MB=MP=MA=MR,
∴∠RMQ=∠PMQ=45°,
∴∠PMR=90°=∠BMA,
在△BMA和△PMR中,
|
∴△BMA≌△PMR(SAS),
∴AB=PR,
∴ON+
| 1 |
| 2 |
| 1 |
| 2 |
即ON+
| 1 |
| 2 |
点评:本题考查了全等三角形的性质和判定,线段垂直平分线的性质,三角形内角和定理,角平分线的性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,题目比较好,难度偏大.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
点A,B,P在同一直线上,下列说法正确的是( )
| A、若AB=2PA,则P是AB的中点 |
| B、若AB=PB,则P是AB的中点 |
| C、若AB=2PB,则P是AB的中点 |
| D、若AB=2PA=2PB,则P是AB的中点 |
已知一条射线OA,若从点O再引两条射线OB和OC,使∠AOB=60°,∠BOC=20°,∠AOC的度数为( )
| A、40° | B、80° |
| C、20° | D、40°或80° |
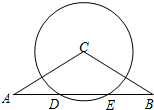 如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.
如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.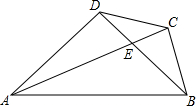 如图,在四边形ABCD中,AC与BD相交于点E,AD=BD,∠ADB=∠ACB=90°,AE=2BC.
如图,在四边形ABCD中,AC与BD相交于点E,AD=BD,∠ADB=∠ACB=90°,AE=2BC. 如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长.
如图:在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=10,BD=6,△AOB的周长为15,求CD的长.