题目内容
已知|ab-2|与|b-1|互为相反数,试求代数式
+
+
+…+
的值.
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2002)(b+2002) |
考点:代数式求值,非负数的性质:绝对值
专题:
分析:由条件可得|ab-2|+|b-1|=0,所以可求得ab=2,b=1,代入可求得a=2,再利用裂项抵消法可求得.
解答:解:
由条件可得|ab-2|+|b-1|=0,所以可求得ab=2,b=1,解得a=2,
所以
+
+
+…+
=
+
+
+…+
=
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
.
由条件可得|ab-2|+|b-1|=0,所以可求得ab=2,b=1,解得a=2,
所以
| 1 |
| ab |
| 1 |
| (a+1)(b+1) |
| 1 |
| (a+2)(b+2) |
| 1 |
| (a+2002)(b+2002) |
=
| 1 |
| 2 |
| 1 |
| (2+1)(1+1) |
| 1 |
| (2+2)(1+2) |
| 1 |
| (2+2002)(1+2002) |
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2003×2004 |
=1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2003 |
| 1 |
| 2004 |
=1-
| 1 |
| 2004 |
=
| 2003 |
| 2004 |
点评:本题主要考查非负数的性质,解题的关键是由条件求得a=2,b=1.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
点A,B,P在同一直线上,下列说法正确的是( )
| A、若AB=2PA,则P是AB的中点 |
| B、若AB=PB,则P是AB的中点 |
| C、若AB=2PB,则P是AB的中点 |
| D、若AB=2PA=2PB,则P是AB的中点 |
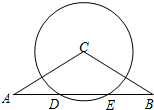 如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.
如图,在等腰△ABC中,CA=CB=6,∠C=120°,⊙C交AB于D、E两点,且AD=DE.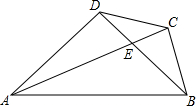 如图,在四边形ABCD中,AC与BD相交于点E,AD=BD,∠ADB=∠ACB=90°,AE=2BC.
如图,在四边形ABCD中,AC与BD相交于点E,AD=BD,∠ADB=∠ACB=90°,AE=2BC.