题目内容
 如图,在△ABC中,AD⊥BC于D,AD=BD,CD=DE,E是AD上一点,连结BE并延长交AC于点F.
如图,在△ABC中,AD⊥BC于D,AD=BD,CD=DE,E是AD上一点,连结BE并延长交AC于点F. (1)求证:BE=AC,BF⊥AC.
(2)连接CE,并延长交AB于P,求证:CP⊥AB.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)利用SAS得到三角形BED与三角形ACD全等,利用全等三角形对应边相等得到BE=AC,且∠EBD=∠CAD,利用对顶角得到∠AEF=∠BED,根据等式的性质得到BF垂直于AC;
(2)由三角形ABD与三角形EDC都为等腰直角三角形,利用等腰直角三角形的性质得到∠PBC=∠PCB=45°,进而得到∠CPB为直角,即可得证.
(2)由三角形ABD与三角形EDC都为等腰直角三角形,利用等腰直角三角形的性质得到∠PBC=∠PCB=45°,进而得到∠CPB为直角,即可得证.
解答:证明:(1)在△BED和△ACD中,
,
∴△BED≌△ACD(SAS),
∴BE=AC,∠EBD=∠CAD,
∵∠EBD+∠BED=90°,∠AEF=∠BED,
∴∠CAD+∠AEF=90°,即∠AFE=90°,
则BF⊥AC;
(2)∵△ABD和△ECD都为等腰直角三角形,
∴∠PBC=∠PCB=45°,
∴∠CPB=90°,即CP⊥AB.
|
∴△BED≌△ACD(SAS),
∴BE=AC,∠EBD=∠CAD,
∵∠EBD+∠BED=90°,∠AEF=∠BED,
∴∠CAD+∠AEF=90°,即∠AFE=90°,
则BF⊥AC;
(2)∵△ABD和△ECD都为等腰直角三角形,
∴∠PBC=∠PCB=45°,
∴∠CPB=90°,即CP⊥AB.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
计算(x-a)(x2+ax+a2)的结果是( )
| A、x3+2ax2-a3 |
| B、x3-a3 |
| C、x3+2a2x-a3 |
| D、x3+2ax2+2a2x-a3 |
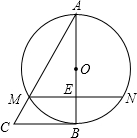 如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=
如图,在△ABC中,以AB为直径的⊙O交AC于点M,弦MN∥BC交AB于点E,且ME=1,AM=2,AE=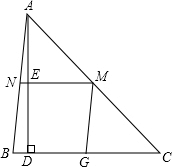 如图所示,有一块锐角三角形的余料ABC,它的边BC=150mm,AB=100mm,要把它加工成菱形零件,使菱形的一边在BC上,其余的两个顶点分别在AB,AC上,加工成的菱形的高ED=51mm,求△ABC的高AD.
如图所示,有一块锐角三角形的余料ABC,它的边BC=150mm,AB=100mm,要把它加工成菱形零件,使菱形的一边在BC上,其余的两个顶点分别在AB,AC上,加工成的菱形的高ED=51mm,求△ABC的高AD.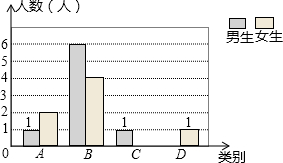 某校九年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表:
某校九年级共有200名学生,在一次数学测验后,为了解本次测验的成绩情况,从中随机抽取了部分学生的成绩进行统计,并制作了如下图表: