题目内容
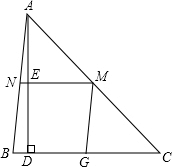如图所示，有一块锐角三角形的余料ABC，它的边BC=150mm，AB=100mm，要把它加工成菱形零件，使菱形的一边在BC上，其余的两个顶点分别在AB，AC上，加工成的菱形的高ED=51mm，求△ABC的高AD．考点：相似三角形的应用,菱形的性质
专题：
分析：设菱形的边长为x，根据菱形的对边平行可得BG∥MN，然后求出△AMN和△ABC相似，利用相似三角形对应边成比例列式求出x，再根据相似三角形对应高的比等于相似比列式计算即可得解．
解答：解：设菱形的边长为x，
∵菱形对边BG∥MN，
∴△AMN∽△ABC，
∴
=
，
即
=
，
解得x=60，
∵△AMN∽△ABC，
∴
=
，
即
=
，
解得AD=85，
答：△ABC的高AD为85mm．
∵菱形对边BG∥MN，
∴△AMN∽△ABC，
∴
| MN |
| BC |
| AN |
| AB |
即
| x |
| 150 |
| 100-x |
| 100 |
解得x=60，
∵△AMN∽△ABC，
∴
| AE |
| AD |
| MN |
| BC |
即
| AD-51 |
| AD |
| 60 |
| 150 |
解得AD=85，
答：△ABC的高AD为85mm．
点评：本题考查了相似三角形的应用，主要利用了相似三角形对应边成比例和相似三角形对应高的比等于相似比的性质，菱形的性质，先求出菱形的边长是解题的关键．
练习册系列答案
相关题目
钟表上，10点10分时，时针与分针的夹角是（ ）
| A、110° | B、120° |
| C、115° | D、125° |
如图，A、B两点被池塘隔开，在AB外任取一点C，连结AC、BC分别取其三等分点M，N（M、N两点均靠近点C）．量得MN=27m，则AB的长是（ ）| A、54m | B、81m |
| C、108m | D、135m |
如图，在△ABC中，AD⊥BC于D，AD=BD，CD=DE，E是AD上一点，连结BE并延长交AC于点F． 
已知，如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DM⊥AB，DN⊥AC，垂足分别为M、N，求证：BM=CN．