题目内容
14.已知关于x的一元二次方程x2-kx+5=0与x2+5x-k=0只有一个公共的实根,求关于x的方程|x2+kx|=|k|所有的实根之和.分析 设一元二次方程x2-kx+5=0与x2+5x-k=0的公共根为t,根据方程解的定义得到t2-kt+5=0与t2+5t-k=0,两方程相减得到(k+5)t=k+5,则t=1,然后把t=1代入x2-kx+5=0得k=6,则|x2+6x|=6,再分类讨论:得出方程x2+6x=6或x2+6x=-6,求出答案即可.
解答 解:设一元二次方程x2-kx+5=0与x2+5x-k=0的公共根为t,
根据题意得t2-kt+5=0与t2+5t-k=0,
∴(k+5)t=k+5,
∵t有唯一的值,
∴k+5≠0,
∴t=1,
把t=1代入x2-kx+5=0得1-k+5=0,解得k=6,
∴|x2+6x|=6,
∴x2+6x=6或x2+6x=-6,
方程x2+6x=6的两根之和为-6,方程x2+6x=-6的两根之和为-6,
∴方程|x2+kx|=|k|所有的实根之和为-12.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.也考查了根与系数的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.若|a|<2,且a是整数,那么a为( )
| A. | 2,1,0 | B. | -2,-1,0,1,2 | C. | -1,0,1 | D. | 0,-1,-2 |
9. 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )
 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )| A. | ∠1与∠2是同旁内角 | B. | ∠1与∠3是内错角 | ||
| C. | ∠1与∠5是同位角 | D. | ∠4与∠5互为邻补角 |
 将杨辉三角中的每一个数换成分数,得到一个如图所示的分数三角形,称为莱布尼茨三角形,第9行第2个数是$\frac{1}{72}$.
将杨辉三角中的每一个数换成分数,得到一个如图所示的分数三角形,称为莱布尼茨三角形,第9行第2个数是$\frac{1}{72}$. 如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
如图,在直角坐标系中,OA=3,OC=4,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
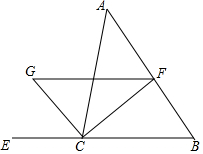 如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数.
如图,CF是∠ACB的平分线,CG是∠ACB外角的平分线,FG∥BC交CG于点G,已知∠A=45°,∠B=55°,求∠FGC和∠FCG的度数.