题目内容
14．计算（1）化简：（1+$\frac{1}{a}$）•$\frac{{a}^{2}}{{a}^{2}-1}$
（2）解不等式组：$\left\{\begin{array}{l}{3（x-1）≤5x+1}\\{\frac{x-1}{2}≥2x-4}\end{array}\right.$．
分析 （1）原式括号中两项通分并利用同分母分式的加法法则计算，约分即可得到结果；
（2）分别求出不等式组中两不等式的解集，找出两解集的公共部分即可．
解答 解：（1）原式=$\frac{a+1}{a}$•$\frac{{a}^{2}}{（a+1）（a-1）}$=$\frac{a}{a-1}$；
（2）$\left\{\begin{array}{l}{3（x-1）≤5x+1①}\\{\frac{x-1}{2}≥2x-4②}\end{array}\right.$，
由①得：x≥-2，
由②得：x≤$\frac{7}{3}$，
则不等式组的解集为-2≤x≤$\frac{7}{3}$．
点评 此题考查了分式的混合运算，以及解一元一次不等式组，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
5．菱形具有、矩形却不具有的性质是（ ）
| A． | 两组对边分别平行 | B． | 对角线互相平分 | ||
| C． | 对角线互相垂直 | D． | 对角线相等 |
9．
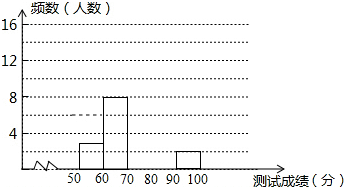为了增强学生环保意识，我区举办了首届“环保知识大赛”，经选拔后有30名学生参加决赛，这30，名学生同事解答50个选择题，若每正确一个选择题得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（4）第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导，则第4组的小宇与小强能同时抽到的概率是多少？
为了增强学生环保意识，我区举办了首届“环保知识大赛”，经选拔后有30名学生参加决赛，这30，名学生同事解答50个选择题，若每正确一个选择题得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：| 组别 | 成绩x分 | 频数（人数） |
| 第1组 | 50≤x＜60 | 3 |
| 第2组 | 60≤x＜70 | 8 |
| 第3组 | 70≤x＜80 | 13 |
| 第4组 | 80≤x＜90 | a |
| 第5组 | 90≤x＜100 | 2 |
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？
（4）第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导，则第4组的小宇与小强能同时抽到的概率是多少？
19．下列运算正确的是（ ）
| A． | 23=6 | B． | （$\frac{1}{2}$）-1=2 | C． | （x3）4=x7 | D． | （π-3）0=0 |
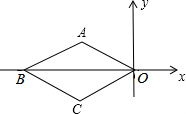如图，菱形ABCO中AO=$\sqrt{3}$，∠AOC=60°，点M第一次从点O移动到点A，第二次从点A移动到点B，第三次从点B移动到点C，第四次从点C移动到点O…照此移动规律，点M第39次移动到的点的坐标是（-$\frac{3}{2}$，-$\frac{\sqrt{3}}{2}$）．
3．为了调查某小区居民的用水情况，随机抽查了若干户家庭月用水量，结果如表：
则关于这若干户家庭的月用水量，中位数是5吨，月平均用水4.6吨．
| 月用水量（吨） | 3 | 4 | 5 | 8 |
| 户数 | 2 | 3 | 5 | 1 |
一个几何体的三视图如图，根据图示的数据计算该几何体的全面积是3π． （结果保留π）．