题目内容
9.某“双选”题的四个选项中有两个正确答案,该题满分为2分,得分规则是:选出两个正确答案且没有多选任何一个错误答案得2分;选出一个正确答案且没有多选任何一个错误答案得1分;不选或所选答案中至少有一个错误答案得0分.(1)任选一个答案,得1分的概率是$\frac{1}{2}$;
(2)任选两个答案,求得2分的概率;
(3)如果只能确认四个选项中的某一个答案是正确的,此时的最佳答题策略是A.
A.只选确认的那一个正确答案
B.除了选择确认的那一个正确答案,再任意选择剩下的三个选项中的一个
C.上述两种答题策略中任选一个.
分析 (1)直接根据概率公式计算;
(2)不妨设四个选项分别为A、B、C、D,其中A、B为正确选项,再列表展示所有6种等可能的结果数,找出AB所占结果数,然后根据概率公式求解;
(3)易得只选确认的那一个正确答案可得1分,再计算除了选择确认的那一个正确答案,再任意选择剩下的三个选项中的一个所得的分数,然后比较两个的得分后确定最佳答题策略.
解答 解:(1)四个选项中有两个正确答案,任选一个答案,选对正确答案的概率=$\frac{2}{4}$=$\frac{1}{2}$;
(2)不妨设四个选项分别为A、B、C、D,其中A、B为正确选项,
列表如下:
共有6种等可能的结果数,其中AB占一个结果数,
所以得2分的概率=$\frac{1}{6}$;
(3)只选确认的那一个正确答案,则可得1分;
若除了选择确认的正确答案A,再从B、C、D中任意选择剩下的三个选项中的一个,则再选正确答案的概率为$\frac{1}{3}$,选错误答案的概率为$\frac{2}{3}$,
所以此时得分=2×$\frac{1}{3}$+0×$\frac{2}{3}$=$\frac{2}{3}$,
所以此时的最佳答题策略是只选确认的那一个正确答案.
故答案为$\frac{1}{2}$,$\frac{1}{6}$,A.
点评 本题考查了列表法与树状图法:利用列表法或树状图展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式计算事件A与B的概率.

练习册系列答案
相关题目
19.下列运算正确的是( )
| A. | 23=6 | B. | ($\frac{1}{2}$)-1=2 | C. | (x3)4=x7 | D. | (π-3)0=0 |
17.为了更好地迎接庐阳区排球比赛,某校积极准备,从全校学生中遴选出21名同学进行相应的排球训练,该训练队成员的身高如下表:
则该校排球队21名同学身高的众数和中位数分别是(单位:cm)( )
| 身高(cm) | 170 | 172 | 175 | 178 | 180 | 182 | 185 |
| 人数(个) | 2 | 4 | 5 | 2 | 4 | 3 | 1 |
| A. | 185,178 | B. | 178,175 | C. | 175,178 | D. | 175,175 |
14.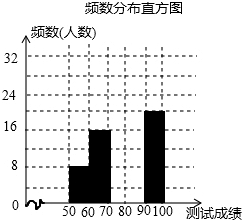 苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
频率分布表:
请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于90分的同学可以获得第53届世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”
 苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:
苏州某中学为了迎接第53届世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:频率分布表:
| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 8 |
| 第2组 | 60≤x<70 | 16 |
| 第3组 | 70≤x<80 | a |
| 第4组 | 80≤x<90 | 32 |
| 第5组 | 90≤x<100 | 20 |
(1)求表中a的值:
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于90分的同学可以获得第53届世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”
 一个几何体的三视图如图,根据图示的数据计算该几何体的全面积是3π. (结果保留π).
一个几何体的三视图如图,根据图示的数据计算该几何体的全面积是3π. (结果保留π).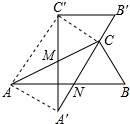 有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( )
有两个全等的含30°角的直角三角板重叠在一起,如图,将△A′B′C′绕AC的中点M转动,斜边A′B′刚好过△ABC的直角顶点C,且与△ABC的斜边AB交于点N,连接AA′、C′C、AC′.若AC的长为2,有以下五个结论:①AA′=1;②C′C⊥A′B′;③点N是边AB的中点;④四边形AA′CC′为矩形;⑤A′N=B′C=$\frac{1}{2}$,其中正确的有( ) 如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC.
如图,点B在线段AC上,点D、E在AC同侧,∠A=∠C=90°,BD⊥BE,AD=BC. 如图,已知线段a,b,∠α,按要求完成下列各小题(保留作图痕迹,不要求写作法)
如图,已知线段a,b,∠α,按要求完成下列各小题(保留作图痕迹,不要求写作法)