题目内容
17.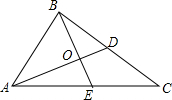 如图,△ABC中,AC、BC上的中线交于点O,且BE⊥AD.若BD=10,BO=8,则AO的长为12.
如图,△ABC中,AC、BC上的中线交于点O,且BE⊥AD.若BD=10,BO=8,则AO的长为12.
分析 先根据勾股定理得到OD的长,再根据重心的性质即可得到AO的长.
解答 解:∵BE⊥AD,BD=10,BO=8,
∴OD=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵AC、BC上的中线交于点O,
∴AO=2OD=12.
故答案为:12.
点评 此题主要考查了勾股定理的应用以及重心的性质,根据已知得出各边之间的关系进而求出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.某商品的进价为每件40元,当售价为每件80元时,每星期可卖出200件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出8件,店里每周利润要达到8450元.若设店主把该商品每件售价降低x元,则可列方程为( )
| A. | (80-x)(200+8x)=8450 | B. | (40-x)(200+8x)=8450 | ||
| C. | (40-x)(200+40x)=8450 | D. | (40-x)(200+x)=8450 |
12.某射击队要从四名运动员中选拔一名运动员参加比赛,选拔赛中每名队员的平均成绩$\overline{x}$与方差S2如下表所示,如果要选择一个成绩高且发挥稳定的人参赛,则应该选( )
| 选手 | 甲 | 乙 | 丙 | 丁 |
| 平均数$\overline{x}$ | 8.5 | 9 | 9 | 8.5 |
| 方差S2 | 1 | 1.2 | 1 | 1.3 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
2.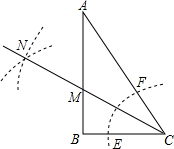 Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
 Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )
Rt△ABC中,∠B=90°∠A=30°.以C为圆心,小于BC长为半径画弧与AC、BC边交于点F、E.分别以E、F为圆心,大于$\frac{1}{2}$EF为半径画弧,两弧交于点N,若BC=$\sqrt{3}$,则点M到AC的距离是( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 3 |
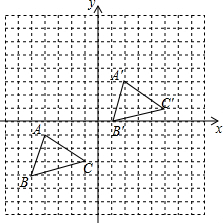 如图所示,将△ABC先向右平移6个单位长度,再向上平移4个单位长度,得到△A′B′C′,△ABC三个顶点的坐标分别为A(-4,-1)、B(-5,-4)、C(-1,-3).
如图所示,将△ABC先向右平移6个单位长度,再向上平移4个单位长度,得到△A′B′C′,△ABC三个顶点的坐标分别为A(-4,-1)、B(-5,-4)、C(-1,-3).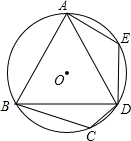 如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E在$\widehat{AD}$上,则∠E=125°.
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=110°.若点E在$\widehat{AD}$上,则∠E=125°.