题目内容
5.在平面直角坐标系中,我们把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(-1,0),把点A经过连续2015次这样的变换得到的点A2015的坐标是($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).分析 分别求得第一、二、三…八次变换后的坐标,得到每8次循环一次.则2014÷8=251…6即可求得结果.
解答 解:由题意第一次旋转后的坐标为($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
第二次旋转后的坐标为(0,-1),
第三次旋转后的坐标为(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),
第四次旋转后的坐标为(1,0),
第五次旋转后的坐标为(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),
第六次旋转后的坐标为(0,1),
第七次旋转后的坐标为($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),
第八次旋转后的坐标为(-1,0)
因为2015÷8=251…7,
所以把点A经过连续2015次这样的变换得到的点A2015的坐标是($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
故答案是:($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$).
点评 本题考查了点的坐标与图形变化-旋转.解答此类找规律的问题的关键是仔细分析题中所给的特征得到规律,再把这个规律应用于解题.

练习册系列答案
相关题目
20.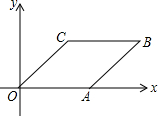 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )
菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )
 菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )
菱形OABC在平面直角坐标系中的位置如图所示,∠AOC=45°,点A的坐标为($\sqrt{2}$,0),则点B的坐标为( )| A. | ($\sqrt{2}$,1) | B. | (1,$\sqrt{2}$) | C. | (1,$\sqrt{2}$+1) | D. | ($\sqrt{2}$+1,1) |
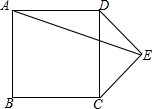 如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=$\frac{\sqrt{5}}{5}$.
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接AE,则sin∠AED=$\frac{\sqrt{5}}{5}$.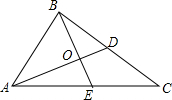 如图,△ABC中,AC、BC上的中线交于点O,且BE⊥AD.若BD=10,BO=8,则AO的长为12.
如图,△ABC中,AC、BC上的中线交于点O,且BE⊥AD.若BD=10,BO=8,则AO的长为12. 学校体育运动会的颁奖台放置于校体育馆内,其主视图如图所示,则其左视图是( )
学校体育运动会的颁奖台放置于校体育馆内,其主视图如图所示,则其左视图是( )


