题目内容
7．
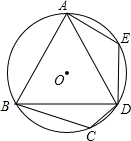如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=110°．若点E在$\widehat{AD}$上，则∠E=125°．
分析 先根据圆内接四边形的性质计算出∠BAD=180°-∠C=70°，再根据等腰三角形的性质和三角形内角和定理计算出∠ABD=55°，然后再根据圆内接四边形的性质可得∠E的度数．
解答 解：∵∠C+∠BAD=180°，
∴∠BAD=180°-110°=70°，
∵AB=AD，
∴∠ABD=∠ADB，
∴∠ABD=$\frac{1}{2}$（180°-70°）=55°，
∵四边形ABDE为圆的内接四边形，
∴∠E+∠ABD=180°，
∴∠E=180°-55°=125°．
故答案为125．
点评 本题考查了圆内接四边形的性质：圆内接四边形的对角互补．也考查了等腰三角形的性质．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
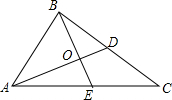如图，△ABC中，AC、BC上的中线交于点O，且BE⊥AD．若BD=10，BO=8，则AO的长为12．
学校体育运动会的颁奖台放置于校体育馆内，其主视图如图所示，则其左视图是（ ）
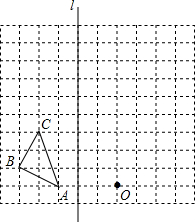如图在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC、直线l和格点O．
12．在△ABC中，∠C=90°，∠A=60°，AC=1，D在BC上，E在AB上，使得△ADE为等腰直角三角形，∠ADE=90°，则BE的长为（ ）
| A． | $4-2\sqrt{3}$ | B． | $2-\sqrt{3}$ | C． | $\sqrt{3}-1$ | D． | $\frac{1}{2}（\sqrt{3}-1）$ |
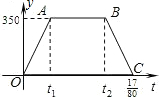沪杭高速铁路已建成通车，某校研究性学习小组以此为课题，在研究列车的行驶速度时，得到一个数学问题．如图，若v是关于t的函数，图象为折线O-A-B-C，其中A（t1，350），B（t2，350），C（$\frac{17}{80}$，0），四边形OABC的面积为70，则t2-t1=$\frac{3}{16}$．
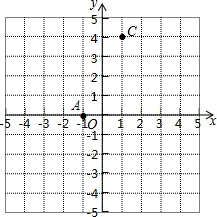如图，A（-1，0），C（1，4），点B在x轴上，且AB=3．