题目内容
9.将抛物线y=4x2向下平移k单位,k>0时,抛物线与x轴有两个交点A、B,此时顶点是C,已知S△ABC=4,求k的值.分析 根据抛物线的平移规律得到平移后的抛物线解析式.设点A(x1,0),B(x2,0),利用根与系数的关系求得AB的距离,由顶点公式求得点C的纵坐标,利用三角形的面积公式,即能求得k值.
解答 解:抛物线y=4x2向下平移k单位后的解析式为:y=4x2-k.
设点A(x1,0),B(x2,0),
∵根与系数的关系得:
x1+x2=0,x1x2=-$\frac{k}{4}$.
∴AB=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{k}$,
又∵顶点C的纵坐标=-k,
∴S△ABC=$\frac{1}{2}$AB•|k|=4,即$\frac{1}{2}$$\sqrt{k}$•|k|=4,
解得k=4.
点评 本题考查了二次函数图象与几何变换.涉及到了二次函数图象的几何变换,根与系数的关系以及三角形的面积,是一道综合性很好的目题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.某企业为了增收节支,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,根据所描出的点猜想y是x的什么函数,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)为了支持希望工程,在实际的销售过程中该公司决定每销售一件工艺品就捐a(a<4)元给希望工程,公司通过销售记录发现,当销售单元价不超过51/件时,每天扣除捐赠后的日销售利润随销售单价x的增大而增大,求a的取值范围.
| 销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
| 每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)为了支持希望工程,在实际的销售过程中该公司决定每销售一件工艺品就捐a(a<4)元给希望工程,公司通过销售记录发现,当销售单元价不超过51/件时,每天扣除捐赠后的日销售利润随销售单价x的增大而增大,求a的取值范围.
18.为了解一批灯泡的使用寿命,从中抽取10只灯泡进行实验,在这个问题中,下列说法正确的是( )
| A. | 这一批灯泡是总体 | B. | 每个灯泡是个体 | ||
| C. | 抽取的10个灯泡是样本 | D. | 抽取的10个灯泡的使用寿命是样本 |
19.以下问题,不适合用全面调查的是( )
| A. | 旅客上飞机前的安检 | B. | 学校招聘教师,对招聘人员的面试 | ||
| C. | 了解一批灯泡的使用寿命 | D. | 了解701班的身高情况 |
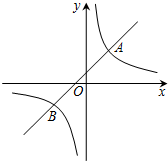 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.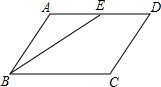 如图,在平行四边形ABCD中,点E为AD的中点,试用无刻度的直尺分别在四边形的内部和外部各画一个与△ABE全等的三角形.
如图,在平行四边形ABCD中,点E为AD的中点,试用无刻度的直尺分别在四边形的内部和外部各画一个与△ABE全等的三角形.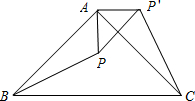 △ABC为直角三角形,∠BAC=90°,将△ABP旋转后与△ACP重合,AP=a,求PP′.
△ABC为直角三角形,∠BAC=90°,将△ABP旋转后与△ACP重合,AP=a,求PP′.