题目内容
19.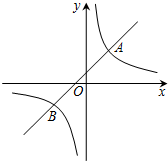 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A(2,3)、B(-3,n)两点.(1)求一次函数和反比例函数的解析式;
(2)根据图象直接写出$kx+b-\frac{m}{x}<0$的x的取值范围.
分析 (1)将A坐标代入反比例函数解析式中求出m的值,即可确定出反比例函数解析式;将B坐标代入反比例解析式中求出n的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出k与b的值,即可确定出一次函数解析式;
(2)根据图象即可得出不等式ax+b<$\frac{m}{x}$的解集.
解答 解:(1)∵反比例函数y=$\frac{m}{x}$经过A(2,3),B(-3,n)两点,
∴可求得m=6,
∴反比例函数的解析式为 y=$\frac{6}{x}$,
将B(2,n)代入y=$\frac{6}{x}$,得n=-2,
∴B(2,-2).
∵一次函数y=ax+b也经过A、B两点,
∴$\left\{\begin{array}{l}{3=2k+b}\\{-2=-3k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
∴一次函数的解析式为 y=x+1,
(2)由图象可知,不等式ax+b<$\frac{m}{x}$的解集为:0<x<2,或x>-3.
点评 此题考查了一次函数与反比例函数的交点问题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,以及不等式和函数的关系,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
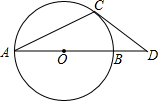 如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=$\sqrt{2}$-1,则∠ACD=112.5°.
如图,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若BD=$\sqrt{2}$-1,则∠ACD=112.5°.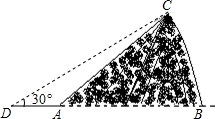 如图,某人在D处测得山顶C的仰角为30°,向前走300米来到山脚A处,测得山坡AC的坡度为i=1:1,求山的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
如图,某人在D处测得山顶C的仰角为30°,向前走300米来到山脚A处,测得山坡AC的坡度为i=1:1,求山的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
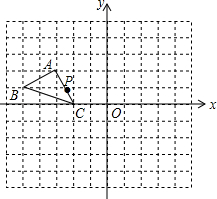 如图,在平面直角坐标系中有三个点A(-3,2)、B(-5,1)、C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).
如图,在平面直角坐标系中有三个点A(-3,2)、B(-5,1)、C(-2,0),P(a,b)是△ABC的边AC上一点,△ABC经平移后得到△A1B1C1,点P的对应点为P1(a+6,b+2).