题目内容
5.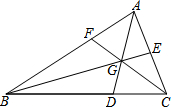 已知:如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是60.
已知:如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是60.
分析 首先根据两个三角形的高相同时,面积的比等于它们的底边的比,求出S△CGD,S△CGE的大小,进而求出S△BCE的大小;然后根据三角形的中线将三角形分成面积相等的两部分,用S△BCE的面积乘以2,求出△ABC的面积是多少即可.
解答 解:∵BD=2DC,
∴S△CGD=$\frac{1}{2}$S△BGD=$\frac{1}{2}$×16=8;
∵E是AC的中点,
∴S△CGE=S△BGE=6,
∴S△BCE=S△BGD+S△CGD+S△CGE
=16+8+6
=30
∴△ABC的面积是:30×2=60.
故答案为:60.
点评 此题主要考查了三角形的面积的求法,以及三角形的中线的特征,要熟练掌握,解答此题的关键是要明确:(1)三角形的中线将三角形分成面积相等的两部分;(2)两个三角形的高相同时,面积的比等于它们的底边的比.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
20. 随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
另外,一卡通普通卡刷卡实行5折优惠,学生卡刷卡实行2.5折优惠.
小明用学生卡乘车,上车时站名上对应的数字是5,下车时站名上对应的数字是22,那么,小明乘车的费用是1元.
 随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:
随着北京公交票制票价调整,公交集团更换了新版公交站牌,乘客在乘车时可以通过新版公交站牌计算乘车费用.新版站牌每一个站名上方都有一个对应的数字,将上下车站站名所对应数字相减取绝对值就是乘车路程,再按照其所在计价区段,参照票制规则计算票价.具体来说:| 乘车路程计价区段 | 0-10 | 11-15 | 16-20 | … |
| 对应票价(元) | 2 | 3 | 4 | … |
小明用学生卡乘车,上车时站名上对应的数字是5,下车时站名上对应的数字是22,那么,小明乘车的费用是1元.
10.设A1,A2,A3,A4是数轴上的四个不同点,若|A1A3|=λ|A1A2|,|A1A4|=η|A1A2|,且$\frac{1}{λ}$+$\frac{1}{η}$=2,则称A3,A4调和分割A1,A2.已知平面上的点C,D调和分割点A,B,则( )
| A. | 点C可能是线段AB的中点 | |
| B. | 点D一定不是线段AB的中点 | |
| C. | 点C,D可能同时在线段AB上 | |
| D. | 点C,D可能同时在线段AB的延长线上 |
15.矩形相邻两边长分别为$\sqrt{2}$,$\sqrt{8}$,则它的周长和面积分别是( )
| A. | $\sqrt{10}$,4 | B. | 2$\sqrt{10}$,4 | C. | 4,3$\sqrt{2}$ | D. | 6$\sqrt{2}$,4 |