题目内容
13.化简下列各式.(1)(-2x-y)(2y+x)-2(x+y)2-2y(x-2y)
(2)($\frac{b}{ab-{b}^{2}}$+$\frac{a+b}{ab-{a}^{2}}$)÷(-$\frac{b}{a}$)2.
分析 (1)先计算多项式乘多项式和单项式乘多项式,然后合并同类项即可;
(2)先把分母因式分解和除法运算化为乘法运算,再把括号内通分,然后进行约分即可.
解答 解:(1)原式=-4xy-2x2-2y2-xy-2x2-4xy-2y2-2xy+4y2
=-11xy-4x2;
(2)原式=[$\frac{b}{b(a-b)}$-$\frac{a+b}{a(a-b)}$]•$\frac{{a}^{2}}{{b}^{2}}$
=$\frac{ab-ab-{b}^{2}}{ab(a-b)}$•$\frac{{a}^{2}}{{b}^{2}}$
=-$\frac{a}{b(a-b)}$
=-$\frac{a}{ab-{b}^{2}}$.
点评 本题考查了分式的混合运算:分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的.最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.也看考查了整式的混合运算.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
 如图,m∥n,那么∠2=50°,那么∠1=50°,∠4=130°.
如图,m∥n,那么∠2=50°,那么∠1=50°,∠4=130°.




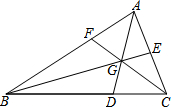 已知:如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是60.
已知:如图,在△ABC中,点D,E,F分别在三边上,E是AC的中点,BD=2DC,AD,BE,CF交于一点G,S△BGD=16,S△AGE=6,则△ABC的面积是60. 如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
如图,△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下: