题目内容
20.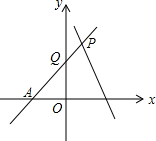 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象,用m,n表示点A,B,P的坐标.
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象,用m,n表示点A,B,P的坐标.
分析 先根据坐标轴上点的坐标特征求A和B点坐标,然后通过解方程$\left\{\begin{array}{l}{y=x+n}\\{y=-2x+m}\end{array}\right.$求P点坐标.
解答 解:当y=0时,x+n=0,解得x=-n,则A(-n,0);
当y=0时,-2x+m=0,解得x=$\frac{m}{2}$,则B($\frac{m}{2}$,0),
解方程$\left\{\begin{array}{l}{y=x+n}\\{y=-2x+m}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{m+n}{3}}\\{y=\frac{m+2n}{3}}\end{array}\right.$,
所以P点坐标为($\frac{m+n}{3}$,$\frac{m+2n}{3}$).
点评 本题考查了两条直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解.若两条直线是平行的关系,那么它们的自变量系数相同,即k值相同.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,AB∥CD,直线EF分别交AB、CD于点E,F,EG平分∠AEF,交CD于G,已知∠1=40°,求∠2的度数.
如图,AB∥CD,直线EF分别交AB、CD于点E,F,EG平分∠AEF,交CD于G,已知∠1=40°,求∠2的度数. 如图,在△ABO中,E是AB的中点,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若△ABO的面积为12,则k=8.
如图,在△ABO中,E是AB的中点,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若△ABO的面积为12,则k=8.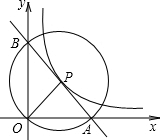 如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=$\frac{k}{x}$(x>0)的图象上任意一点,以P为圆心,PO为半径的圆与x轴、y轴分别交于点A、B.
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=$\frac{k}{x}$(x>0)的图象上任意一点,以P为圆心,PO为半径的圆与x轴、y轴分别交于点A、B. 如图,l1反映了某公司产品的销售收入与销售量之间的关系;l2反映了该公司产品的销售成本与销售量之间的关系,请根据图象提供的信息,求直线l1和直线l2对应的函数解析式.
如图,l1反映了某公司产品的销售收入与销售量之间的关系;l2反映了该公司产品的销售成本与销售量之间的关系,请根据图象提供的信息,求直线l1和直线l2对应的函数解析式.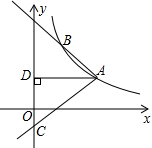 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),射线AB与反比例函数的图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),射线AB与反比例函数的图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.