题目内容
11. 如图,在△ABO中,E是AB的中点,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若△ABO的面积为12,则k=8.
如图,在△ABO中,E是AB的中点,双曲线y=$\frac{k}{x}$(k>0)经过A、E两点,若△ABO的面积为12,则k=8.
分析 设出点B的坐标和点A的纵坐标,根据△ABO的面积为12,用b表示h,求出点A的坐标,根据E是AB的中点,求出点E的坐标,代入双曲线求出k的值.
解答 解:设B为(b,0),A纵坐标为h,
由题意得,
$\frac{1}{2}$×b×h=12,
h=$\frac{24}{b}$,
∴点A的坐标为:($\frac{kb}{24}$,$\frac{24}{b}$),
则点E的坐标为:($\frac{b+\frac{kb}{24}}{2}$,$\frac{12}{b}$),
代入双曲线可得:k=8.
故答案为:8.
点评 本题考查的是反比例函数系数k的几何意义,求出点E的坐标是解题的关键,解答时,注意:k=xy.

练习册系列答案
相关题目
1.2月26日,国家统计局发布《2014年国民经济和社会发展统计公报》.《公报》显示,初步核算,全年国内生产总值约为640000亿元,用科学记数法可表示为( )亿元.
| A. | 6.3×105亿元 | B. | 6.3×106亿元 | C. | 6.4×105亿元 | D. | 0.64×106亿元 |
19.下列事件是随机事件的是( )
| A. | 购买一张福利彩票,中奖 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 太阳每天从东边升起 | |
| D. | 在一个仅装着白球和黑球的袋中摸出红球 |
16. 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
 如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )
如图,直线l1∥l2,l3⊥l4,∠1=44°,那么∠2的度数( )| A. | 46° | B. | 44° | C. | 36° | D. | 22° |
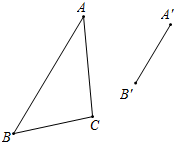 如图,已知△ABC和△A′B′C′是位似比为2的位似三角形,且AB的对应边是A′B′,请用尺规作图,将△A′B′C′补充完整(可不写作法,但保留作图痕迹).
如图,已知△ABC和△A′B′C′是位似比为2的位似三角形,且AB的对应边是A′B′,请用尺规作图,将△A′B′C′补充完整(可不写作法,但保留作图痕迹).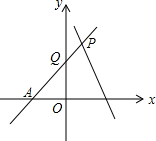 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象,用m,n表示点A,B,P的坐标.
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象,用m,n表示点A,B,P的坐标.