题目内容
9.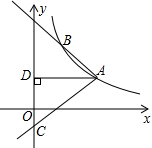 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),射线AB与反比例函数的图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(2$\sqrt{3}$,1),射线AB与反比例函数的图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.(1)求k的值;
(2)求tan∠DAC的值;
(3)求经过A,C两点的直线的解析式.
分析 (1)根据反比例函数图象上点的坐标特征易得k=2$\sqrt{3}$;
(2)作BH⊥AD于H,如图1,根据反比例函数图象上点的坐标特征确定B点坐标为(1,2$\sqrt{3}$),则AH=2$\sqrt{3}$-1,BH=2$\sqrt{3}$-1,可判断△ABH为等腰直角三角形,所以∠BAH=45°,得到∠DAC=∠BAC-∠BAH=30°,根据特殊角的三角函数值得tan∠DAC=$\frac{\sqrt{3}}{3}$;
(3)由于AD⊥y轴,则OD=1,AD=2$\sqrt{3}$,然后在Rt△OAD中利用正切的定义可计算出CD=2,易得C点坐标为(0,-1),于是可根据待定系数法求出直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x-1.
解答  解:(1)把A(2$\sqrt{3}$,1)代入y=$\frac{k}{x}$ 得k=2$\sqrt{3}$×1=2$\sqrt{3}$;
解:(1)把A(2$\sqrt{3}$,1)代入y=$\frac{k}{x}$ 得k=2$\sqrt{3}$×1=2$\sqrt{3}$;
(2)作BH⊥AD于H,如图,
把B(1,a)代入反比例函数解析式y=$\frac{2\sqrt{3}}{x}$得a=2$\sqrt{3}$,
∴B点坐标为(1,2$\sqrt{3}$),
∴AH=2$\sqrt{3}$-1,BH=2$\sqrt{3}$-1,
∴△ABH为等腰直角三角形,
∴∠BAH=45°,
∵∠BAC=75°,
∴∠DAC=∠BAC-∠BAH=30°,
∴tan∠DAC=tan30°=$\frac{\sqrt{3}}{3}$;
(3)∵AD⊥y轴,
∴OD=1,AD=2$\sqrt{3}$,
∵tan∠DAC=$\frac{CD}{DA}$=$\frac{\sqrt{3}}{3}$,
∴CD=2,
∴OC=1,
∴C点坐标为(0,-1),
设直线AC的解析式为y=kx+b,
把A(2$\sqrt{3}$,1)、C(0,-1)代入y=kx+b得$\left\{\begin{array}{l}{2\sqrt{3}k+b=1}\\{b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-1}\end{array}\right.$,
∴直线AC的解析式为y=$\frac{\sqrt{3}}{3}$x-1.
点评 本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征和待定系数法求一次函数解析式;理解坐标与图形的性质;同时要熟悉三角函数.

 口算题天天练系列答案
口算题天天练系列答案| A. | 购买一张福利彩票,中奖 | |
| B. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| C. | 太阳每天从东边升起 | |
| D. | 在一个仅装着白球和黑球的袋中摸出红球 |
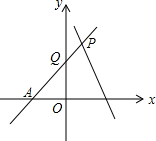 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象,用m,n表示点A,B,P的坐标.
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象,用m,n表示点A,B,P的坐标.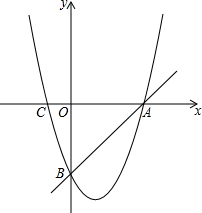 如图,抛物线y=x2-2x+n与直线y=x-3相交于A、B两点(点A在x轴上,点B在y轴上),与x轴的另一个交点为点C.
如图,抛物线y=x2-2x+n与直线y=x-3相交于A、B两点(点A在x轴上,点B在y轴上),与x轴的另一个交点为点C. 如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )
如图是由四个相同的小正方体组成的立体图形,它的俯视图为( )


