题目内容
15.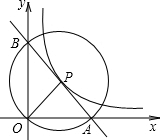 如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=$\frac{k}{x}$(x>0)的图象上任意一点,以P为圆心,PO为半径的圆与x轴、y轴分别交于点A、B.
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数y=$\frac{k}{x}$(x>0)的图象上任意一点,以P为圆心,PO为半径的圆与x轴、y轴分别交于点A、B.(1)判断点P是否在线段AB上,并说明理由;
(2)若S△ABO=12,求k的值;
(3)Q是反比例函数y=$\frac{k}{x}$的图象上异于点P的另一点,请以Q为圆心,QO为半径画圆,⊙Q与x轴、y轴分别交于点M、N,连接AN、BM,求证:AN∥BM.
分析 (1)判断出AB是⊙O直径,即可得到点P在线段AB上;
(2)过点P作PP1⊥x轴,PP2⊥y轴,由题意可知PP1、PP2是△AOB的中位线,判断出S△BP2P:S△BOA=1:4,求出S四边形OP1PP2=6,即可求出k的值;
(3)如图,连接MN,则MN过点Q,连接AN,EM,且S△MON=S△AOB=12,故OA•OB=OM•ON,即$\frac{OA}{OM}$=$\frac{ON}{OB}$,得到△AON∽△MOB.
解答 解:(1)点P在线段AB上,理由如下:
∵点O在⊙P上,且∠AOB=90°,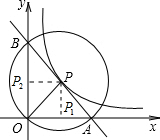
∴AB是⊙P的直径,
∴点P在线段AB上;
(2)过点P作PP1⊥x轴,PP2⊥y轴,由题意可知PP1、PP2是△AOB的中位线,
∵S△BP2P:S△BOA=1:4,
∴S△BP2P=$\frac{1}{4}$S△AOB=$\frac{1}{4}$×12=3,
同理,S△AP1P=3,
∴S四边形OP1PP2=12-6=6,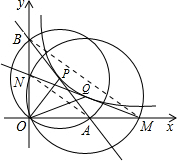
∴k=6;
(3)如图,连接MN,则MN过点Q,连接AN,EM,且S△MON=S△AOB=12,
∴OA•OB=OM•ON,
∴$\frac{OA}{OM}$=$\frac{ON}{OB}$,
∵∠AON=∠MOB,
∴△AON∽△MOB,
∴∠OAN=∠OMB,
∴AN∥MB.
点评 本题考查了反比例函数综合题,熟悉反比例函数k的几何意义、相似三角形的判定与性质、平行线的判定与性质是解题的关键.

练习册系列答案
相关题目
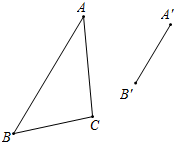 如图,已知△ABC和△A′B′C′是位似比为2的位似三角形,且AB的对应边是A′B′,请用尺规作图,将△A′B′C′补充完整(可不写作法,但保留作图痕迹).
如图,已知△ABC和△A′B′C′是位似比为2的位似三角形,且AB的对应边是A′B′,请用尺规作图,将△A′B′C′补充完整(可不写作法,但保留作图痕迹).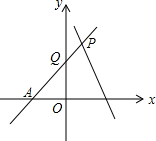 如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象,用m,n表示点A,B,P的坐标.
如图,直线PA是一次函数y=x+n(n>0)的图象,直线PB是一次函数y=-2x+m(m>n)的图象,用m,n表示点A,B,P的坐标.