题目内容
11.在小学,我们曾学过圆柱的体积计算公式:v=πR2h (R是圆柱底面半径,h为圆柱的高).现有一个长方形,长为2cm.宽为1cm,分别以它的两边所在的直线为轴旋转一周.得到的几何体的体积分别是多少?它们之间有何关系?分析 根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.
解答 解:分两种情况:
①绕长所在的直线旋转一周得到圆柱体积为:π×12×2=2π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×22×1=4π(cm3).
故它们的体积分别为2πcm3或4πcm3.
关系:绕宽所在的直线旋转一周得到圆柱体积是绕长所在的直线旋转一周得到圆柱体积的2倍.
点评 本题考查了点、线、面、体,圆柱体的体积的求法,注意分情况讨论,难度适中.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
6.无论k取何值时,关于x,y的方程(k-1)x+(k+1)y-k+3=0均有解$\left\{\begin{array}{l}{x=m}\\{y=n}\end{array}\right.$,则m2015+n2015的值为( )
| A. | 0 | B. | -2 | C. | 22015-1 | D. | 22015-1 |
1.下列关于抛物线y=-x2-2的结论,正确的是( )
| A. | 与x轴有两个交点 | B. | 开口向上 | ||
| C. | 与y轴的交点坐标(0,2) | D. | 顶点坐标是(0,-2) |
 如图所示,多边形ABCFDE中,AB=8,BC=12,ED+DF=13,AE=CF,则多边形ABCFDE的面积是57.75.
如图所示,多边形ABCFDE中,AB=8,BC=12,ED+DF=13,AE=CF,则多边形ABCFDE的面积是57.75.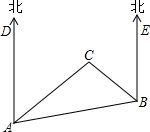 如图所示,C岛在A岛的北偏东35°方向上,B岛在A岛北偏东75°方向上,C岛在B岛的北偏西30°方向上,从C岛看A、B两岛的视角∠ACB是多少度?
如图所示,C岛在A岛的北偏东35°方向上,B岛在A岛北偏东75°方向上,C岛在B岛的北偏西30°方向上,从C岛看A、B两岛的视角∠ACB是多少度? 如图,在△ABC中,∠C=90°,DE⊥AB,垂足为D,交AC于E,若BC=BD,求证:AE+DE=AC.
如图,在△ABC中,∠C=90°,DE⊥AB,垂足为D,交AC于E,若BC=BD,求证:AE+DE=AC.