题目内容

2．如图所示，多边形ABCFDE中，AB=8，BC=12，ED+DF=13，AE=CF，则多边形ABCFDE的面积是57.75．

分析 运用拼图的方法，构造一个正方形，用大正方形的面积-小正方形的面积，即可得出所求多边形的面积．

解答 解：运用拼图的方法，构造一个正方形，如图所示：
大正方形的边长为12+8=20，小正方形的边长ED+DF=13，
∴多边形ABCFDE的面积=$\frac{1}{4}$（大正方形的面积-小正方形面积）=$\frac{1}{4}$（202-132）=57.75．
故答案为：57.75．

点评 本题考查了正方形的判定与性质；熟练掌握正方形的判定与性质，运用拼图的方法，构造一个正方形是解决问题的关键．

练习册系列答案
相关题目
12．如图，某海滨浴场岸边可近似地看成直线，位于岸边A处的救生员发现海中B处有人求救，1号救生员以6m/秒的速度从A处跑300米到距离B最近的D处，然后游向B处．他在海中游进的速度为2m/秒，∠BAD=45°．
（1）根据以上条件分析1号救伤员的选择是否有道理，并说明理由．
（2）若2号救生员跑到C处，再游向B处，且∠BCD=65°，问：哪名救生员先赶到B处救人？（参考数据：sin65°≈0.9，cos65°≈0.4，tan65°≈2.1，$\sqrt{2}$≈1.4，且为计算方便，计算过程中均保留1位小数）
13．下列说法正确的是（　　）
A．-2是-8的立方根B．1的平方根是1C．-1的平方根是-1D．$\sqrt{16}$的平方根是4
10．若|x-2|+|y-2|=0，则x+y的值为4．
17．大于-2而小于3的整数有4个．
7．解方程：
（1）$\frac{{{x^2}-4x}}{{{x^2}-1}}+1=\frac{2x}{x+1}$．        
（2）$\frac{x-3}{x-2}+1=\frac{3}{2-x}$．
14．（1）计算：（$\sqrt{2}$+1）0-（-$\frac{1}{2}$）2-2-2；   
（2）计算：$\sqrt{8}$+（-$\frac{1}{3}$）-1-|$\sqrt{2}$-1|
11．在小学，我们曾学过圆柱的体积计算公式：v=πR2h （R是圆柱底面半径，h为圆柱的高）．现有一个长方形，长为2cm．宽为1cm，分别以它的两边所在的直线为轴旋转一周．得到的几何体的体积分别是多少？它们之间有何关系？
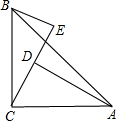12．如图，在△ABC中，∠ACB=90°，AC=BC，BE⊥CE于点E，AD⊥CE于点D，AD=7cm，BE=3cm，求DE的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网