题目内容
6.无论k取何值时,关于x,y的方程(k-1)x+(k+1)y-k+3=0均有解$\left\{\begin{array}{l}{x=m}\\{y=n}\end{array}\right.$,则m2015+n2015的值为( )| A. | 0 | B. | -2 | C. | 22015-1 | D. | 22015-1 |
分析 该题实际上是求x、y的值;将原方程转化为k(x+y-1)=x-y-3的形式,根据未知数的对应系数相等进行解答即可.
解答 解:由(k-1)x+(k+1)y-k+3=0,得
kx-x+ky-y-k+3=0,即k(x+y-1)=x-y-3.
∵无论k取何值时,关于x,y的方程(k-1)x+(k+1)y-k+3=0均有解$\left\{\begin{array}{l}{x=m}\\{y=n}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x+y-1=0}\\{x-y-3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
∴m=2,n=-1,
∴m2015+n2015=22015-1.
故选:C.
点评 本题考查了二元一次方程的解.把已知方程变形为k(x+y-1)=x-y-3的形式是解题的难点.

练习册系列答案
相关题目
16.下列语句:
①顶角、底角都相等的两个等腰三角形一定全等;
②两个等边三角形一定是全等图形;
③如果两个三角形全等,它们的形状和大小一定都相同;
④三个角一一对应相等的两个三角形一定全等.
其中错误的说法有( )
①顶角、底角都相等的两个等腰三角形一定全等;
②两个等边三角形一定是全等图形;
③如果两个三角形全等,它们的形状和大小一定都相同;
④三个角一一对应相等的两个三角形一定全等.
其中错误的说法有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
1.如果a>b,那么下列不等式中,错误的是( )
| A. | a-2>b-2 | B. | -2a>-2b | C. | $\frac{a}{2}>\frac{b}{2}$ | D. | -3a<-3b |
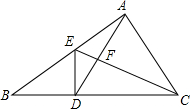 如图,△ABC中,D是BC的中点,且AD=AC,DE⊥BC,交AB于点E,CE交AD于点F.求证:$\frac{AB}{AC}=\frac{CF}{DF}$.
如图,△ABC中,D是BC的中点,且AD=AC,DE⊥BC,交AB于点E,CE交AD于点F.求证:$\frac{AB}{AC}=\frac{CF}{DF}$.