题目内容
10.以下是某市自来水价格调整表:自来水价格调整表(部分) 单位:元/立方米
| 用水类别 | 现行水价 | 拟调整后水价 |
| 一、居民生活用水 | 0.72 | |
| 1.一户一表 | ||
| 第一阶梯:月用水量在 0~30立方米/户 | 0.82 | |
| 第二阶梯:月用水量超过 30立方米/户 | 1.23 | |
| 2.集体表 | 略 |
| A. |  | B. | 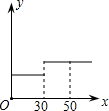 | C. |  | D. |  |
分析 根据水费等于单价乘用水量,30立方米内单价低,水费增长的慢,超过30立方米的部分水费单价高,水费增长快,可得答案.
解答 解:30立方米内每立方是0.82元,超过30立方米的部分每立方是1.23元,
调整水价后某户居民月用水量x(立方米)与应交水费y(元)的函数图象先增长慢,后增长快,C符合题意,
故选:C.
点评 本题考查了函数图象,单价乘以用水量等于水费,单价低水增长的慢,单价高水费增长的快.

练习册系列答案
相关题目
20.一蓄水池有水40m3,如果每分钟放出2m3的水,水池里的水量y(m3)与放水时间t(分)有如下关系:
下列结论中正确的是( )
| 放水时间(分) | 1 | 2 | 3 | 4 | … |
| 水池中水量(m3) | 38 | 36 | 34 | 32 | … |
| A. | y随t的增加而增大 | |
| B. | 放水时为20分钟时,水池中水量为8m3 | |
| C. | y与t之间的关系式为y=40-t | |
| D. | 放水时为18分钟时,水池中水量为4m3 |
1.计算3x2•(-2x)3的结果是( )
| A. | -18x5 | B. | -24x5 | C. | -24x6 | D. | -18x6 |
5.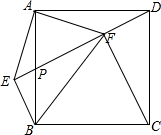 如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:
如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:
①△ABE≌△ADF;②FB=AB;③FC=EF;④BF⊥AF;⑤PF=EP+EB.
其中正确的命题个数有( )
 如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:
如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP的延长线于点E,连接AE,过点A作AF⊥AE,AF交DP于点F,连接BF、CF.下列结论:①△ABE≌△ADF;②FB=AB;③FC=EF;④BF⊥AF;⑤PF=EP+EB.
其中正确的命题个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.已知二次函数y=x2-2mx+m2+3(m为常数),下列结论正确的是( )
| A. | 当m=0时,二次函数图象的顶点坐标为(0,0) | |
| B. | 当m<0时,二次函数图象的对称轴在y轴右侧 | |
| C. | 若将该函数图象沿y轴向下平移6个单位,则平移后图象与x轴两交点之间的距离为$2\sqrt{3}$ | |
| D. | 设二次函数的图象与y轴交点为A,过A作x轴的平行线,交图象于另一点B,抛物线的顶点为C,则△ABC的面积为m3 |
19.如图1,E为矩形ABCD边AD上一点,点P从点B出发沿折线BE-ED-DC运动到点C时停止,点Q从点B出发沿BC运动到点C时停止,它们运动的速度都是1cm/s.若P,Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2).已知y与t的函数图象如图2,则下列结论错误的是( )


| A. | 当t=11s时,y=40cm2 | B. | BE=10cm | ||
| C. | 当0≤t≤10时,y=$\frac{2}{5}$t2 | D. | 当t=16s时,∠PBQ=30° |
12.利用加减消元法解方程组$\left\{\begin{array}{l}{2x+5y=3①}\\{5x-3y=6②}\end{array}\right.$,下列做法正确的是( )
| A. | 要消去y,可以将①×5+②×2 | B. | 要消去x,可以将①×3+②×(-5) | ||
| C. | 要消去y,可以将①×5+②×3 | D. | 要消去x,可以将①×(-5)+②×2 |
 如图,与∠1构成同位角的是∠B,,与∠2构成同旁内角的是∠1.
如图,与∠1构成同位角的是∠B,,与∠2构成同旁内角的是∠1.