题目内容
10.k取2值时,方程$\left\{\begin{array}{l}{x-y-k=0}\\{{x}^{2}-8y=0}\end{array}\right.$有一个实数解.分析 首先通过消元把二元二次方程组转化成一元二次方程,然后利用一元二次方程的判别式得到关于k的方程,解方程即可求出k.
解答 解:$\left\{\begin{array}{l}{x-y-k=0①}\\{{x}^{2}-8y=0②}\end{array}\right.$,
由①得y=x-k ③,
把③代入②得,
x2-8x+8k=0,
∵方程组只有一个实数解,
∴△=(-8)2-4×8k=64-32k=0,
∴k=2.
故答案为2.
点评 此题考查了判别式的应用、方程组的解法等知识,考查运算能力及转化思想.

练习册系列答案
相关题目
9.下列各组的运算结果相等的是( )
| A. | 34和43 | B. | -($\frac{1}{2}$)3和(-$\frac{1}{2}$)3 | C. | -22和 (-2 )2 | D. | |-3|和-|-3| |
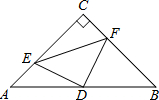 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF. 已知:如图,AB=CD,AD=BC.求证:AB∥CD.
已知:如图,AB=CD,AD=BC.求证:AB∥CD. 如图,直线EF过边长为5的正方形ABCD的顶点B,点A、C到直线EF的距离分别是3和4,则五边形AEFCD的面积是37.
如图,直线EF过边长为5的正方形ABCD的顶点B,点A、C到直线EF的距离分别是3和4,则五边形AEFCD的面积是37. 已知Rt△ABC中,∠ACB=90°,中线BD、CE交于G点,∠BGC=90°,CG=2,则BC=2$\sqrt{3}$.
已知Rt△ABC中,∠ACB=90°,中线BD、CE交于G点,∠BGC=90°,CG=2,则BC=2$\sqrt{3}$.