题目内容
13.⊙O的半径OA=2,弦AB、AC的长为2$\sqrt{2}$、2$\sqrt{3}$,则∠BAC的度数为15°或75°.分析 分两种情况,如图1与图2所示,过O作OD⊥AB,OE⊥AC,连接OA,利用垂径定理及锐角三角函数定义分别求出∠OAC与∠OAB的度数,即可求出∠BAC度数.
解答 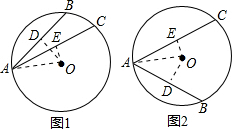 解:分两种情况考虑:
解:分两种情况考虑:
如图1所示,过O作OD⊥AB,OE⊥AC,连接OA,
∴AE=$\frac{1}{2}$AC=$\sqrt{3}$,AD=$\frac{1}{2}$AB=$\sqrt{2}$,且∠OAE=30°,∠OAB=45°,
∴∠BAC=15°;
如图2所示,过O作OD⊥AB,OE⊥AC,连接OA,
∴AE=$\frac{1}{2}$AC=$\sqrt{3}$,AD=$\frac{1}{2}$AB=$\sqrt{2}$,且∠OAE=30°,∠OAB=45°,
∴∠BAC=75°,
故答案为:15°或75°
点评 此题考查了垂径定理,以及锐角三角函数定义,熟练掌握垂径定理是解本题的关键.

练习册系列答案
相关题目
10.式子-mn与(-m)n的正确判断是( )
| A. | 这两个式子互为相反数 | B. | 这两个式子是相等的 | ||
| C. | 当n为奇数时,它们相等 | D. | n为偶数时它们相等 |
1.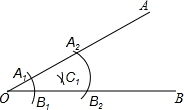 如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )
如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )
 如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )
如图,已知∠AOB=30°,以O为圆心、a为半径画弧交OA、OB于A1、B1,再分别以A1、B1为圆心、a为半径画弧交于点C1,以上称为一次操作.再以C1为圆心a为半径重新操作,得到C2.重复以上步骤操作,记最后一个两弧的交点(离点O最远)为CK,则点CK到射线OB的距离为( )| A. | $\frac{a}{2}$ | B. | $\frac{\sqrt{3}}{2}$a | C. | a | D. | $\sqrt{3}$a |
8.小明家买了一辆小轿车,小明连续记录了一周每天行驶的路程:
请你用学过的知识解决下面的问题:
(1)小明家的轿车每月(按30天计算)要行驶多少千米?
(2)若每行驶100千米需汽油8升,汽油每升6.70元,请你算出小明家一年(按12个月计算)的汽油费用大约是多少元.
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
| 路程(千米) | 30 | 33 | 27 | 37 | 35 | 53 | 30 |
(1)小明家的轿车每月(按30天计算)要行驶多少千米?
(2)若每行驶100千米需汽油8升,汽油每升6.70元,请你算出小明家一年(按12个月计算)的汽油费用大约是多少元.
18.下列哪个式子表示(-x)(-x)(-x)的结果( )
| A. | -3x3 | B. | -3x | C. | -x3 | D. | 3x |
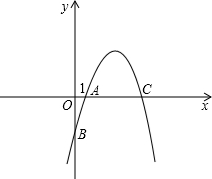 如图,抛物线y=-x2+5x+n与x轴交点A(1,0),另一交点C,与y轴交于点B.
如图,抛物线y=-x2+5x+n与x轴交点A(1,0),另一交点C,与y轴交于点B.