题目内容
 如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A,∠B平分线的交点,试求点P到AB边的距离.
如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A,∠B平分线的交点,试求点P到AB边的距离.考点:角平分线的性质
专题:
分析:连接PC,作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,由角平分线的性质可知PD=PE=PF,可设PD=PE=PF=r,再由三角形的面积公式即可得出结论.
解答: 解:连接PC,作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,
解:连接PC,作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,
∵点P是∠A,∠B平分线的交点,
∴PD=PE=PF.
设PD=PE=PF=r,
∵AB=5,BC=3,AC=4,
∴
AC•BC=
AC•r+
BC•r+
AB•r=
r(AC+BC+AB),即
×4×3=
r×(4+3+5),解得r=1,
∴点P到AB边的距离为1.
 解:连接PC,作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,
解:连接PC,作PD⊥AB,PE⊥AC,PF⊥BC,垂足分别为D、E、F,∵点P是∠A,∠B平分线的交点,
∴PD=PE=PF.
设PD=PE=PF=r,
∵AB=5,BC=3,AC=4,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴点P到AB边的距离为1.
点评:本题考查的是角的平分线,熟知角平分线上的点到角两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
 如图所示,数轴上点A,B,C各表示有理数a,b,c.
如图所示,数轴上点A,B,C各表示有理数a,b,c.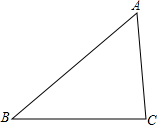 作图并解析:
作图并解析: 如图,在△ABC中,AD是∠BAC的平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=
如图,在△ABC中,AD是∠BAC的平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD= 如图,在△ABC中,∠C=90°,AC=BC,AD是∠A的平分线,交CB于点D.
如图,在△ABC中,∠C=90°,AC=BC,AD是∠A的平分线,交CB于点D. 如图所示,在长为a厘米、宽为
如图所示,在长为a厘米、宽为 如图,已知:BD=CE=AF,DE=DF=EF,△DEF为正三角形.求证:△ABC为正三角形.
如图,已知:BD=CE=AF,DE=DF=EF,△DEF为正三角形.求证:△ABC为正三角形.