题目内容
 如图,已知:BD=CE=AF,DE=DF=EF,△DEF为正三角形.求证:△ABC为正三角形.
如图,已知:BD=CE=AF,DE=DF=EF,△DEF为正三角形.求证:△ABC为正三角形.考点:等边三角形的判定与性质
专题:证明题
分析:利用反证法,先假设△ABC中有两边相等,可证明△ABC为等边三角形,再假设△ABC中各边不相等,可证明假设不成立,即可△ABC为等边三角形.
解答:证明:如果AB.BC.AC有两条边AB.AC相等,则AE=BD,BF=AD,ED=DF;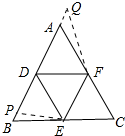
在△AFD和△BDE中,
∴△AFD≌△BDE(SSS),
∴∠A=∠B,
∵AB=AC,
∴∠A=∠B=∠C,
∴△ABC是等边三角形;
若∠A、∠B、∠C各不相等,
则这个三角形中至少有一个角大于60°,一个角小于60°,
设∠A>60°,∠B<60°,
在BA及延长线上分别取点P、Q,使得∠DPE=60°,∠AQF=60°,
∵∠ADE+∠FDE+∠EDP=180°,
且△DPE的内角和为180°,
∴∠DPE=∠FDE=60°,
∴∠DEP=∠ADF,
在△QDF和△PED中,
∴△QDF≌△PED(AAS),
∴DQ=PE,
∵∠BPE为钝角,
∴BE>PE,
∴AD=BE>DQ显然不成立,
∴△ABC必为等边三角形.

在△AFD和△BDE中,
|
∴△AFD≌△BDE(SSS),
∴∠A=∠B,
∵AB=AC,
∴∠A=∠B=∠C,
∴△ABC是等边三角形;
若∠A、∠B、∠C各不相等,
则这个三角形中至少有一个角大于60°,一个角小于60°,
设∠A>60°,∠B<60°,
在BA及延长线上分别取点P、Q,使得∠DPE=60°,∠AQF=60°,
∵∠ADE+∠FDE+∠EDP=180°,
且△DPE的内角和为180°,
∴∠DPE=∠FDE=60°,
∴∠DEP=∠ADF,
在△QDF和△PED中,
|
∴△QDF≌△PED(AAS),
∴DQ=PE,
∵∠BPE为钝角,
∴BE>PE,
∴AD=BE>DQ显然不成立,
∴△ABC必为等边三角形.
点评:本题考查了全等三角形的判定与性质;本题运用反证法证明是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
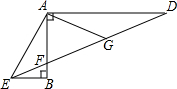 如图,∠ABE=∠BAD=90°,∠AED=2∠BED,点G是DF的中点,若BE=1,AG=4.
如图,∠ABE=∠BAD=90°,∠AED=2∠BED,点G是DF的中点,若BE=1,AG=4. 如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A,∠B平分线的交点,试求点P到AB边的距离.
如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A,∠B平分线的交点,试求点P到AB边的距离. 如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱?
如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱?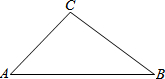 如图,在△ABC中,∠A=45°,AC=
如图,在△ABC中,∠A=45°,AC=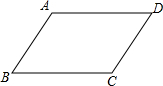 如图,已知?ABCD,求证:∠A=∠C,∠B=∠D(要求:不添加辅助线)
如图,已知?ABCD,求证:∠A=∠C,∠B=∠D(要求:不添加辅助线)
 如图,Rt△ABC和以AB为边的正方形ABEF,已知∠ACB=90°,AC=12,BC=5,求正方形ABEF的面积.
如图,Rt△ABC和以AB为边的正方形ABEF,已知∠ACB=90°,AC=12,BC=5,求正方形ABEF的面积.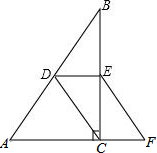 如图,在△ABC中,∠ACB=90°,DE是△ABC的中位线,点F在AC的延长线上,且CF=
如图,在△ABC中,∠ACB=90°,DE是△ABC的中位线,点F在AC的延长线上,且CF=