题目内容
 如图,在△ABC中,AD是∠BAC的平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=
如图,在△ABC中,AD是∠BAC的平分线,AB=8cm,AC=6cm,则S△ABD:S△ACD=考点:角平分线的性质
专题:
分析:作DE⊥AB于E,DF⊥AC于F,由角平分线的性质可知,DE=DF,再由三角形的面积公式求解即可.
解答: 解:作DE⊥AB于E,DF⊥AC于F,
解:作DE⊥AB于E,DF⊥AC于F,
∵AD是∠BAC的平分线,
∴DE=DF
∴S△ABD:S△ACD=
AB•DE:
AC•DF=AB:AC=8:6=4:3.
故答案为:4:3.
 解:作DE⊥AB于E,DF⊥AC于F,
解:作DE⊥AB于E,DF⊥AC于F,∵AD是∠BAC的平分线,
∴DE=DF
∴S△ABD:S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:4:3.
点评:本题考查的是角平分线的性质及三角形的面积公式,由角平分线的性质及三角形的面积公式作出辅助线是解答此题的关键.

练习册系列答案
相关题目
 用一块长24.84分米的长方形铁皮,按如图剪下两个相等的圆形后正好做成一个圆柱形油桶,求这个油桶的容积(接头忽略不计)
用一块长24.84分米的长方形铁皮,按如图剪下两个相等的圆形后正好做成一个圆柱形油桶,求这个油桶的容积(接头忽略不计)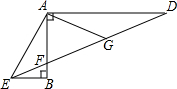 如图,∠ABE=∠BAD=90°,∠AED=2∠BED,点G是DF的中点,若BE=1,AG=4.
如图,∠ABE=∠BAD=90°,∠AED=2∠BED,点G是DF的中点,若BE=1,AG=4. 如图,四边形OABC是矩形,且∠AOx=120°,CO=
如图,四边形OABC是矩形,且∠AOx=120°,CO= 如图,△ABC中,∠C=90°,AD是角平分线,AC=8,AD=
如图,△ABC中,∠C=90°,AD是角平分线,AC=8,AD= 如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A,∠B平分线的交点,试求点P到AB边的距离.
如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A,∠B平分线的交点,试求点P到AB边的距离. 如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱?
如图,某会展中心在一次会展期间准备在楼梯上铺地毯,已知楼梯的高BC为5m,斜面AC为13m,每一级楼梯宽AD为2m,地毯的价格为每平方米20元,铺完这个楼梯至少需要多少元钱? 如图,Rt△ABC和以AB为边的正方形ABEF,已知∠ACB=90°,AC=12,BC=5,求正方形ABEF的面积.
如图,Rt△ABC和以AB为边的正方形ABEF,已知∠ACB=90°,AC=12,BC=5,求正方形ABEF的面积.