题目内容
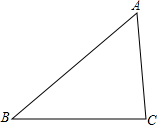 作图并解析:
作图并解析:(1)如图,过点C作AB的垂线,垂足为D,过D作DE∥BC交AC于点E,过E作EF∥AB,交BC于F.
(2)若∠B=35°,试求∠EDC的度数.
考点:作图—基本作图
专题:
分析:(1)根据过一个点作已知直线的垂线的方法作CD⊥AB;作∠ADE=∠B可得DE∥BC,再作∠DEF=∠ADE可得EF∥AB;
(2)根据垂线定义可得∠ADC=∠BDC=90°,再根据平行线的性质可得∠ADE=∠B=35°,进而可得∠EDC的度数.
(2)根据垂线定义可得∠ADC=∠BDC=90°,再根据平行线的性质可得∠ADE=∠B=35°,进而可得∠EDC的度数.
解答:解:(1)如图所示:
 ;
;
(2)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵DE∥BC,
∴∠ADE=∠B=35°,
∴∠EDC=90°-35°=55°.
 ;
;(2)∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵DE∥BC,
∴∠ADE=∠B=35°,
∴∠EDC=90°-35°=55°.
点评:此题主要考查了基本作图,关键是掌握做一个角等于已知角的方法,内错角相等,两直线平行.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
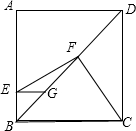 如图,在正方形ABCD中,点E、G分别在边AB、对角线BD上,EG∥AD,F为GD的中点,连接FC,利用勾股定理的逆定理,证明EF⊥FC.
如图,在正方形ABCD中,点E、G分别在边AB、对角线BD上,EG∥AD,F为GD的中点,连接FC,利用勾股定理的逆定理,证明EF⊥FC.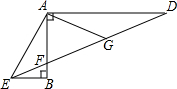 如图,∠ABE=∠BAD=90°,∠AED=2∠BED,点G是DF的中点,若BE=1,AG=4.
如图,∠ABE=∠BAD=90°,∠AED=2∠BED,点G是DF的中点,若BE=1,AG=4. 如图,⊙O的两条割线PAB交圆于A、B.割线PCD交圆于C、D.求证:(
如图,⊙O的两条割线PAB交圆于A、B.割线PCD交圆于C、D.求证:(
 如图,四边形OABC是矩形,且∠AOx=120°,CO=
如图,四边形OABC是矩形,且∠AOx=120°,CO= 如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A,∠B平分线的交点,试求点P到AB边的距离.
如图,在△ABC中,AB=5,BC=3,AC=4,点P是∠A,∠B平分线的交点,试求点P到AB边的距离.