题目内容

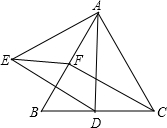
6．已知：在△ABC中，D、E为AC、AB上的点，BD、CE相交于O，取AB的中点F，联结OF，若AD=$\frac{1}{2}$CD，AE=$\frac{1}{2}$BE
求证：OF∥BC．

分析 连接DE，根据平行线分线段成比例定理得到DE∥BC，根据线段中点的概念得到$\frac{EF}{FB}$=$\frac{1}{3}$，证明结论．

解答 证明：连接DE，
∵AD=$\frac{1}{2}$CD，AE=$\frac{1}{2}$BE，
∴DE∥BC，
∴$\frac{EO}{OC}$=$\frac{DE}{BC}$=$\frac{AD}{AC}$=$\frac{1}{3}$，
∵点F是AB的中点，AE=$\frac{1}{2}$BE，
∴$\frac{EF}{FB}$=$\frac{1}{3}$，
∴OF∥BC．

点评 本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．

练习册系列答案
相关题目
18．下列图标中，是轴对称的是（　　）
A．B．C．D．
19．方程$\frac{x-1}{x+3}$=$\frac{1}{2}$的解为（　　）
A．x=0B．x=2C．x=-5D．x=5
16．从-3，-2，-1，1，2，3六个数中任取一个数为k，使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解，且关于x的一次函数y=kx+3不经过第四象限的概率是（　　）
A．$\frac{1}{3}$B．$\frac{1}{4}$C．$\frac{1}{5}$D．$\frac{1}{6}$
1．如图1，点P是平面直角坐标系中第一象限内任意一点，PA⊥y轴，PB⊥x轴，垂足分别为A、B，反比例函数y=$\frac{k}{x}$（x＞0）交线段PA于点C（不与P重合），交线段PB于点D（不与P重合），连接CD和AB．
①CD不一定平行于AB；
②$\frac{PC}{CA}$=$\frac{PD}{DB}$；    
③若P（a，b）且k=$\frac{ab}{2}$，则把△PCD沿CD折叠后P点一定落在AB上；
④如图2，过点C作CE⊥x轴，过点D作DF⊥y轴，垂足分别为E、F，若两个阴影部分面积相等，则D为PB中点．
其中正确的是②③④（把所有正确结论的序号都选上）．
11．如果2x=7，那么x=3.5．
18．某网店在网上销每一种新型热水袋100件，每件售价40元，打出的促销广告是：若一次性购买不超过10件时，售价不变；若一次性购买超过10件时，每多买1件，每件售价均降低0.2元．已知热水袋进价是每件20元，设顾客一次性购买热水袋x（件）时，该网店获利为y（元）．
（1）求y（元）与x（件）之间的函数关系式，并写出自变量x的取值范围；
（2）顾客一次性购买多少件热水袋时，该网店获利最大？最大利润是多少？
15．二次函数y=（x-1）2+k分别与x轴、y轴交于A、B、C三点，点A在点B的左侧，直线y=-$\frac{2}{3}$x+2经过点B，且与y轴交于点D．
（1）如图1，求k的值；
（2）如图2，在第一象限的抛物线上有一动点P，连接AP，过P作PE⊥x轴于点E，过E作EF⊥AP于点F，过点D作平行于x轴的直线分别与直线FE、PE交于点G、H，设点P的横坐标为t，线段GH的长为d，求d与t的函数关系式，并直接写出t的取值范围；
（3）在（2）的条件下，过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N，tan∠MEA=$\frac{3}{2}$，点K为第四象限抛物线上一点，且在对称轴左侧，连接KA，在射线KA上取一点R，连接RM，过点K作KQ⊥AK交PE的延长线于Q，连接AQ、HK，若∠RAE-∠RMA=45°，△AKQ与△HKQ的面积相等，求点R的坐标．
16．如图，已知在等边△ABC中，AD，CF分别为边CB，BA上的中线，以AD为边作等边△ADE．求证：
（1）四边形CDEF是平行四边形；
（2）EF平分∠AED．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网