题目内容
16.从-3,-2,-1,1,2,3六个数中任取一个数为k,使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解,且关于x的一次函数y=kx+3不经过第四象限的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
分析 首先利用分式方程的知识求得当k=-3,-2,-1,3,使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解,再利用一次函数的性质,求得当k=1,2,3时,关于x的一次函数y=kx+2不经过第四象限,再利用概率公式即可求得答案.
解答 解:∵方程两边同乘以(x+1),
∴k-1=(k-2)(x+1),
∴当k=2或k=1时,关于x的分式方程$\frac{k-1}{x+1}$=k-2无解,
∴当k=-3,-2,-1,3,使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解;
∵关于x的一次函数y=kx+2不经过第四象限,
∴k>0,
∴当k=1,2,3时,关于x的一次函数y=kx+2不经过第四象限,
∴得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解,且关于x的一次函数y=kx+2不经过第四象限的有3;
∴使得关于x的分式方程$\frac{k-1}{x+1}$=k-2有解,且关于x的一次函数y=kx+2不经过第四象限的概率为:$\frac{1}{6}$.
故选D.
点评 此题考查了概率公式的应用、一次函数的性质以及分式方程.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
6.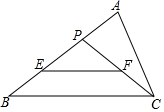 如图:P为△ABC边AB上一点且AP:BP=1:2,E、F分别是PB,PC的中点,△ABC、△PEF的面积分别为S和S1,则S和S1的关系式( )
如图:P为△ABC边AB上一点且AP:BP=1:2,E、F分别是PB,PC的中点,△ABC、△PEF的面积分别为S和S1,则S和S1的关系式( )
 如图:P为△ABC边AB上一点且AP:BP=1:2,E、F分别是PB,PC的中点,△ABC、△PEF的面积分别为S和S1,则S和S1的关系式( )
如图:P为△ABC边AB上一点且AP:BP=1:2,E、F分别是PB,PC的中点,△ABC、△PEF的面积分别为S和S1,则S和S1的关系式( )| A. | S1=$\frac{1}{3}$S | B. | S1=$\frac{1}{4}$S | C. | S1=$\frac{2}{3}$S | D. | S1=$\frac{1}{6}$S |
7.下列把多项式分解因式正确的是( )
| A. | -ma-m=-m(a-1) | B. | x2-y2=(x-y)2 | C. | a2+3a+9=(a+3)2 | D. | 2x2-2=2(x+1)(x-1) |
4.下列式子计算结果为2x2的是( )
| A. | x+x | B. | x•2x | C. | (2x)2 | D. | 2x6÷x3 |
11.一辆汽车沿倾斜角α的斜坡前进1000米,则它上升的高度是( )
| A. | 1000•sinα米 | B. | $\frac{1000}{sinα}$米 | C. | 1000•cosα米 | D. | $\frac{1000}{cosα}$米 |
1.据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338600000亿次,数字338600000用科学记数法可表示为( )
| A. | 3.386×109 | B. | 0.3386×109 | C. | 33.86×107 | D. | 3.386×108 |
3.某商场计划购进甲、乙两种计算器共1200个,这两种计算器的进价、售价如表:
(1)在这次进货中商场恰好花费46000元,请求出甲、乙两种计算器各购进了多少个?
(2)设该商场购进甲种计算器t个,商场销售完这批计算器可获利y元,请求出y关于t的函数解析式;
(3)如何进货才能使商场在销售完这批计算器时获利最多,且不超过进货价的30%?此时利润为多少元?
| 进价(元/只) | 售价(元/只) | |
| 甲型 | 25 | 30 |
| 乙型 | 45 | 60 |
(2)设该商场购进甲种计算器t个,商场销售完这批计算器可获利y元,请求出y关于t的函数解析式;
(3)如何进货才能使商场在销售完这批计算器时获利最多,且不超过进货价的30%?此时利润为多少元?
 已知:在△ABC中,D、E为AC、AB上的点,BD、CE相交于O,取AB的中点F,联结OF,若AD=$\frac{1}{2}$CD,AE=$\frac{1}{2}$BE
已知:在△ABC中,D、E为AC、AB上的点,BD、CE相交于O,取AB的中点F,联结OF,若AD=$\frac{1}{2}$CD,AE=$\frac{1}{2}$BE