题目内容
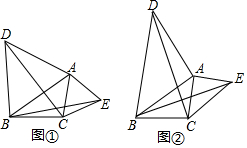
16. 如图,已知在等边△ABC中,AD,CF分别为边CB,BA上的中线,以AD为边作等边△ADE.求证:
如图,已知在等边△ABC中,AD,CF分别为边CB,BA上的中线,以AD为边作等边△ADE.求证:(1)四边形CDEF是平行四边形;
(2)EF平分∠AED.
分析 (1)由等边三角形的性质证出DE=CF,DE∥CF,即可得出结论;
(2)由平行四边形的性质和等边三角形的性质证出∠AEF=30°=∠DEF即可.
解答 证明:(1)∵△ABC是等边三角形,AD,CF分别为边CB,BA上的中线,
∴AD=CF,AD⊥BC,∠BCF=30°,
∵△ADE是等边三角形,
∴DE=AD,∠ADE=60°,
∴∠BDE=90°-60°=30°=∠BCF,
∴DE=CF,DE∥CF,
∴四边形CDEF是平行四边形;
(2)∵四边形CDEF是平行四边形,
∴EF∥CD,
∴∠FED=∠BCF=30°,
∵△ADE是等边三角形,
∴∠AED=60°,
∴∠AEF=30°=∠DEF,
∴EF平分∠AED.
点评 此题考查了平行四边形的判定与性质、等边三角形的性质.熟练掌握等边三角形的性质,证明四边形是平行四边形是解决问题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
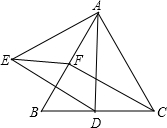
 已知:在△ABC中,D、E为AC、AB上的点,BD、CE相交于O,取AB的中点F,联结OF,若AD=$\frac{1}{2}$CD,AE=$\frac{1}{2}$BE
已知:在△ABC中,D、E为AC、AB上的点,BD、CE相交于O,取AB的中点F,联结OF,若AD=$\frac{1}{2}$CD,AE=$\frac{1}{2}$BE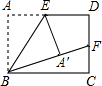 如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=2$\sqrt{2}$.
如图,在矩形ABCD中,E、F分别是AD、CD的中点,沿着BE将△ABE折叠,点A刚好落在BF上,若AB=2,则AD=2$\sqrt{2}$.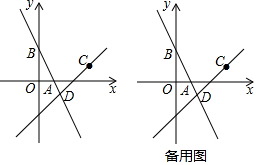
 如图,已知AB∥CD,∠A=49°,∠C=29°,则∠E的度数为20°.
如图,已知AB∥CD,∠A=49°,∠C=29°,则∠E的度数为20°. 甲、乙两人在一段笔直的公路AB上行走,甲从A地出发前往B地,乙从B地出发前往A地,已知A、B两地相距4千米,乙比甲晚出发20分钟,甲、乙两人离A地的距离y(千米)与甲出发后经过的时间x(分钟)之间的函数关系如图所示.
甲、乙两人在一段笔直的公路AB上行走,甲从A地出发前往B地,乙从B地出发前往A地,已知A、B两地相距4千米,乙比甲晚出发20分钟,甲、乙两人离A地的距离y(千米)与甲出发后经过的时间x(分钟)之间的函数关系如图所示.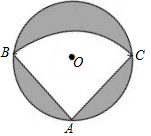 有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.